Changement de référentiel
-
Ssupertux dernière édition par
Bonjour,
Je cherche de l'aide pour le problème suivant. J'ai un robot qui se trouve dans une pièce rectangulaire. Je connais son orientation par rapport au plus grand mur (angle theta dans la figure), et je connais les coordonnées du centre M de la pièce dans le référentiel du robot : Xm, Ym
Je cherche à calculer maintenant les coordonnées du robot (Ur, Vr) dans le référentiel de la pièce (centre M: origine, axes u, v parallèles au petit mur et grand mur, respectivement).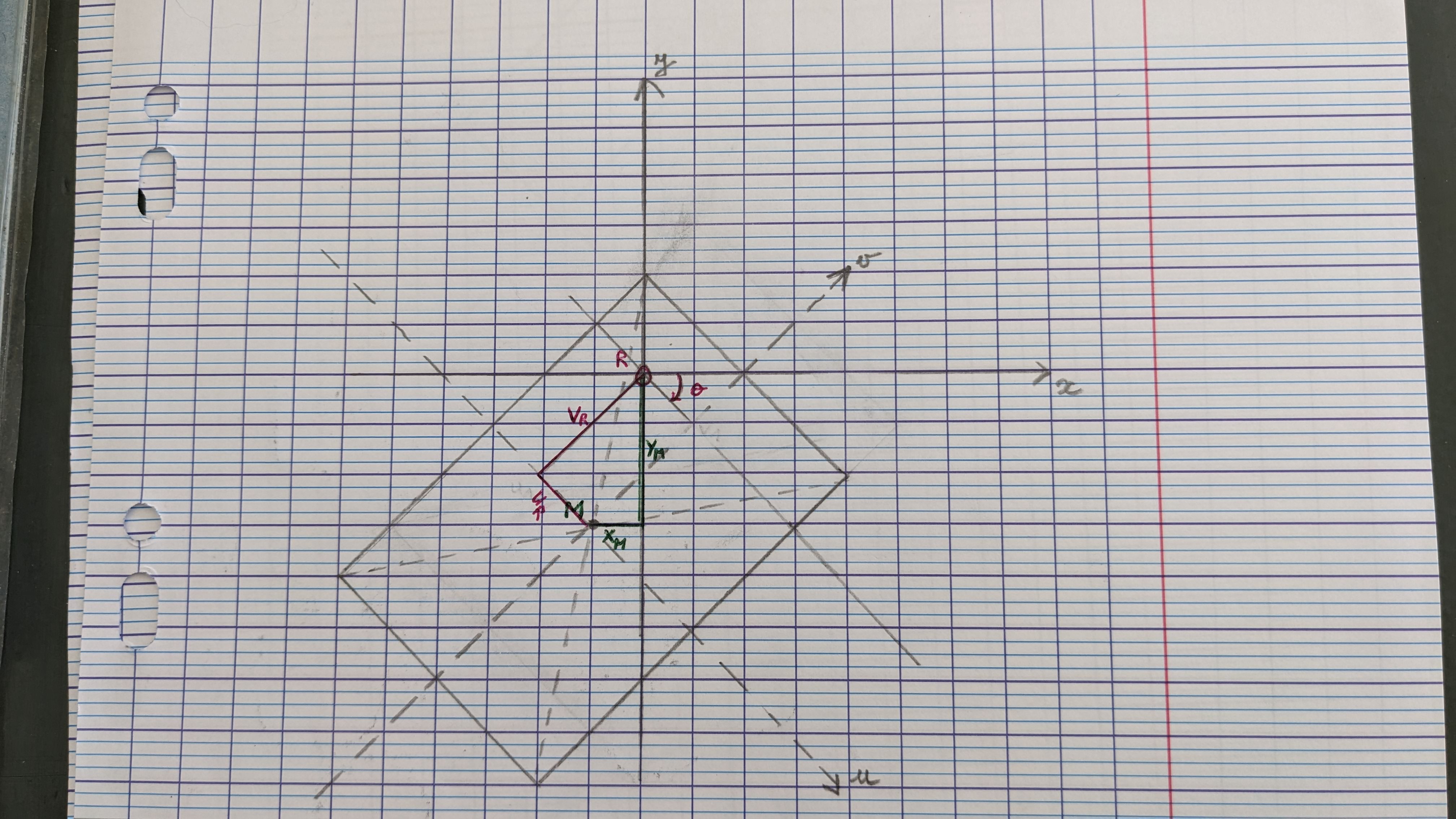
Toute aide sera appréciée

-
BBlack-Jack dernière édition par Black-Jack
Bonjour,
Si j'ai bien interprété la question, je trouve :
vR=XM.sin(θ)−YM.cos(θ)v_R = X_M.sin(\theta) - Y_M.cos(\theta)vR=XM.sin(θ)−YM.cos(θ)
uR=−XM.cos(θ)−YM.sin(θ)u_R = - X_M.cos(\theta) - Y_M.sin(\theta)uR=−XM.cos(θ)−YM.sin(θ)Avec les conventions habituelles sur les mesures d'angles.
Soit donc : angle positif dans le sens inverse des aiguilles d'une montre(Donc sur le dessin, le theta dessiné est négatif)
Exemple sur le dessin :
XM = -1
YM = -3
theta = -Pi/4on calcule :
vR = -1sin(-Pi/4)+3cos(-Pi/4) = 2,828... (2racine carrée de 2)
uR = 1cos(-Pi/4) + 3.sin(-Pi/4) = -1,414 (- racine carrée de 2)
-
Ssupertux dernière édition par
super ! merci beaucoup
donc ces formules fonctionnent quelque soit l'orientation et la position du robot dans la pièce ?
comment tu arrives à ces formules ?
-
BBlack-Jack dernière édition par
Copie du ticket de tram avec ma rédaction :
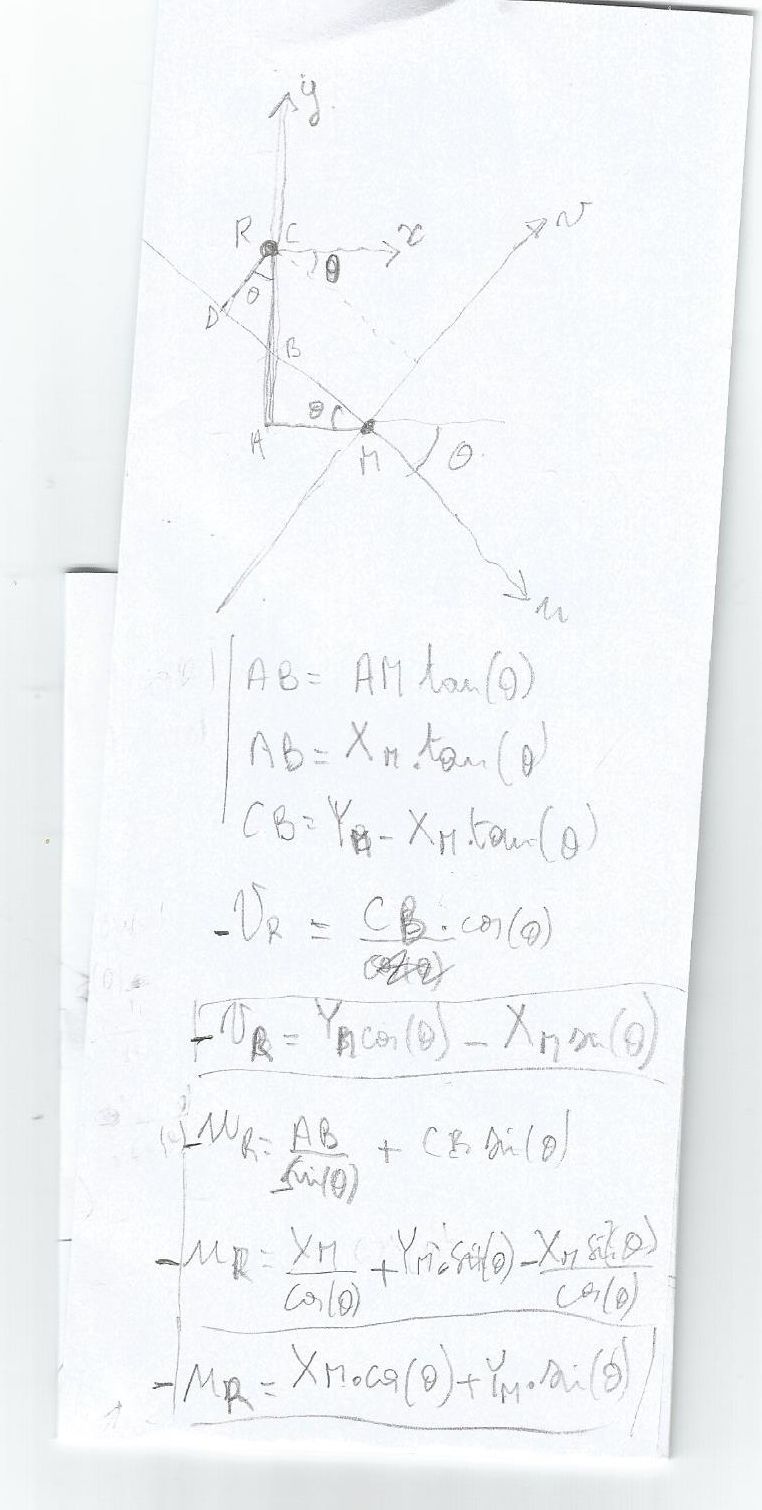
-
Ssupertux dernière édition par
@Black-Jack merci

j'ai essayé de retrouver les formules, j'ai la même chose au final sauf que Ur et Vr sont inversées...
je pense que c'est dû à un signe négatif à un moment mais je suis un peu perdu, quand on calcule les tangentes il faut prendre en compte l'orientation de theta peut-être ? (pour moi je raisonne juste en terme de longueurs, donc tout est positif)
-
Ssupertux dernière édition par
@supertux j'avance, j'arrive à retrouver Ur, mais j'ai un problème de signe pour Vr

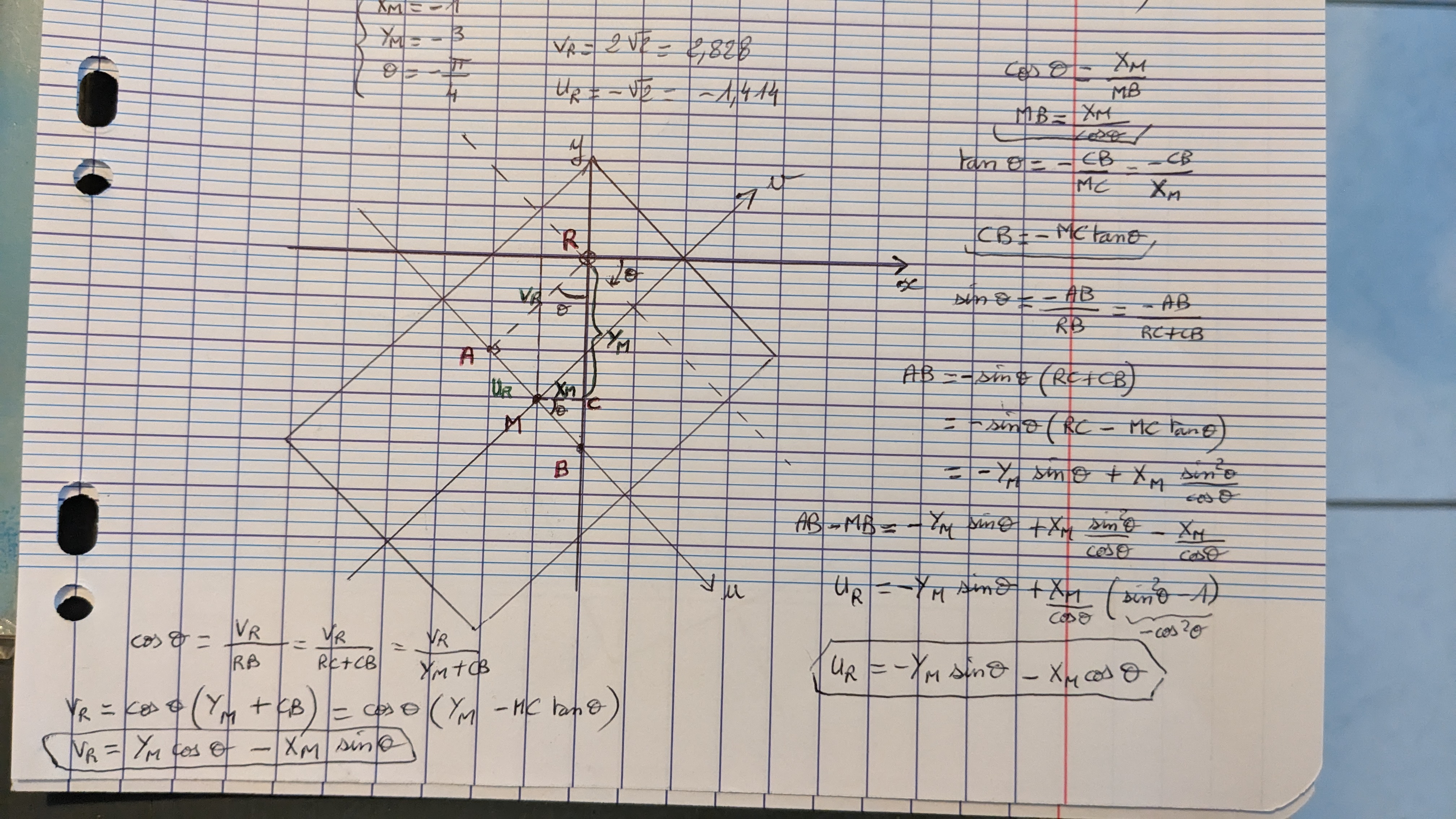
Je m'embrouille entre les longueurs et les coordonnées.
On est d'accord que tan(theta) = -CB / MC ? (signe - vu que theta est négatif)
mais si je remplace MC par Xm ?
-
BBlack-Jack dernière édition par
Bonjour,
cos(θ)=∣AR∣∣RC∣+∣CB∣cos(\theta) = \frac{|AR|}{|RC|+|CB|}cos(θ)=∣RC∣+∣CB∣∣AR∣ (1)
Avec:
∣AR∣=VR|AR| = V_R∣AR∣=VR car ∣AR∣|AR|∣AR∣ > 0 et VRV_RVR > 0
et ∣RC∣=−YM|RC| = -Y_M∣RC∣=−YM car ∣RC∣|RC| ∣RC∣ > 0 et YMY_MYM < 0
et ∣CB∣=XM.tan(θ)|CB| = X_M.tan(\theta)∣CB∣=XM.tan(θ) car ∣CB∣|CB|∣CB∣ > 0 et XM.tan(θ)X_M.tan(\theta)XM.tan(θ) > 0 puisque XMX_MXM et tan(θ)tan(\theta)tan(θ) tous les deux < 0
(1) →\to→ cos(θ)=VR−YM+XM.tan(θ)cos(\theta) = \frac{V_R}{-Y_M+X_M.tan(\theta)}cos(θ)=−YM+XM.tan(θ)VRVR=−YM.cos(θ)+XM.sin(θ)V_R = -Y_M.cos(\theta) + X_M.sin(\theta)VR=−YM.cos(θ)+XM.sin(θ)
-
Ssupertux dernière édition par
Merci !
J'ai repris les calculs en faisant bien attention aux signes, et je trouve les mêmes formules
