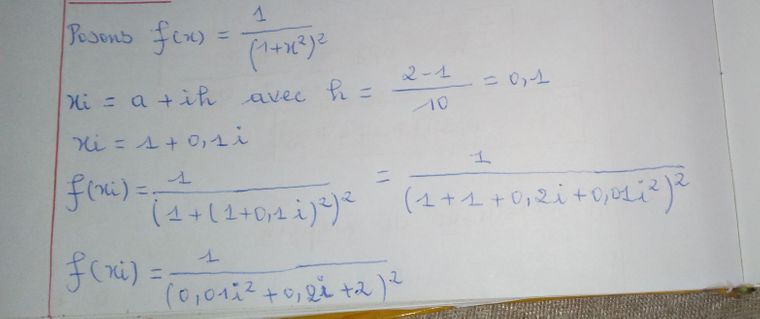Intégration numérique ( Méthode de Simpson )

Bonjour comment vous allez. j'ai du mal à m'ensortir dans cet exercice . J'aimerais avoir besoin d'aide de votre part.
Soit J = ∫ (1 à 2 ) 1/( 1 + x^2 )^2
Donner une valeur Jn de J par la méthode de SIMPSON.
Faire 10 subdivisions.
Nous avons l'exercice avec le Prof mais j'ai du mal à comprendre.

@medou-coulibaly Bonjour,

Indique les premiers calculs et ceux que tu ne comprends pas.

@Noemi

@medou-coulibaly

Quelle formule d'approximation de Simpson utilises tu ?

@Noemi

Bonjour,

@medou-coulibaly , je te mets un lien (vidéo) pour t'expliquer la méthode (méthode de Simson dite (1/3)).
C'est la plus simple et c'est celle qu'utilise ton cours.
Je trouve l'explication très claire et agréable à écouter.
Ecoute la plusieurs fois pour être sûr de bien comprendre.
Dans cette vidéo, il y a le calcul de $I_h$ mais pas la borne supérieure de l'erreur.

https://www.youtube.com/watch?v=N1TMup2tNaU

Lorsque tu as bien compris la méthode de calcul, je te conseille cette seconde vidéo.
Regarde la méthode de Simson 1/3
https://www.youtube.com/watch?v=qO8bfl83HFI

L'erreur est prévue et il y a un exemple numérique traité.

Concrètement, pour faire les calculs, le mieux est d'utiliser un tableur sinon le travail est fastidieux...

Bonne lecture.

@medou-coulibaly , une remarque

Le cours que tu indiques, ainsi que les vidéos proposées, utilise la formule de Simson et la majoration de l'erreur, toutes faites, sans les démonstrations.
Les formules sont à retenir.

Si tu veux avoir une petite idée des démonstrations, tu peux regarder ici :
http://serge.mehl.free.fr/anx/meth_simpson.html

@mtschoon Bonjour madame j'ai compris je vais écouter

@mtschoon Bonjour madame j'ai très écouté la vidéo et j'ai bien compris merci beaucoup à vous

Bonsoir,

C'est parfait @medou-coulibaly si maintenant la démarche est maintenant claire pour toi.

@mtschoon Bonjour madame oui oui merci beaucoup à vous