Spd spi isometrie nombre complexe

Le plan Pest rapporté au repère orthonormé (0, e, e₂) Soit les points M, A et B de coordonnées respectives (x, y), (2:0) et (0; 1). Soit F l'application affine de P qui, au point M d'affixe z = x + iy associe le point M' d'affive z telle que z' = $2−i2(z‾−2)2-\frac{i}{2}(\overline{z}-2)$
1 Montrer que Fest une similitude plane indirecte. F peut-elle être une isométrie ?
F peu etre une isometrie svp ?*

@omah a dit dans Spd spi isometrie nombre complexe :

Le plan Pest rapporté au repère orthonormé (0, e, e₂) Soit les points M, A et B de coordonnées respectives (x, y), (2:0) et (0; 1). Soit F l'application affine de P qui, au point M d'affixe z = x + iy associe le point M' d'affixe z telle que z' = $2−i2(z‾−2)2-\frac{i}{2}(\overline{z}-2)$
1 Montrer que Fest une similitude plane indirecte. F peut-elle être une isométrie ?
( $z′=−12iz‾+3z'=\frac{-1}{2}i\overline{z}+3$ forme de l'écriture complexe dune SPI; et par conséquent F ne peut pas etre une isometrie car $a^2+b^2¥1$ )

Elements caracteristiques de F
Rapport k=1/2
Centre B(8;2/3)
Axe (jai pas trouver las mm equation en résolvant le systeme )
Quelles sont les droites globalement invariantes par F ? Quelles sont les droites orthogonales a leurs transformées par F?
Aidez moi avec la 3. Question svp
Bonsoir

verifiez moi mes calcules svp et des pistes pour le reste

@omah , bonjour,
(Formule de politesse à ne pas oublier)

Effectivement, les éléments caractéristiques de F sont inextacts ( à par le rapport de la similitude)

Tu as fait une erreur en transformant la forme complexe de la similitude.

$z′=2−i2(zˉ−2)z'=2-\dfrac{i}{2}(\bar z-2)$
$z′=2−i2(zˉ)+iz'=2-\dfrac{i}{2}(\bar z)+i$
$z′=−i2zˉ+(2+i)\boxed{z'=-\dfrac{i}{2}\bar z+(2+i)}$

Expression de la forme $z′=azˉ+bz'=a\bar z +b$ avec $a≠0a\ne 0$ donc $F$ est bien une similitude plane indirecte.
$∣a∣=∣−i2∣=12|a|=|-\dfrac{i}{2}|=\dfrac{1}{2}$

Le rapport de $F$ est bien $12\dfrac{1}{2}$

Le point invariant est le point tel que $z^{'} = z$

Refais tes calculs et tu dois trouver $x = 2$ et $y = 0$ c'est à dire $z = 2$ .
Le point invariant est donc le point $A$ donné dans l'énoncé $A (2, 0)$

Pour déterminer l'axe $(Δ)(\Delta)$ de la similitude, j'ignore ce qu'indique ton cours...(regarde-le)
Une méthode commode :
M étant un point quelconque du plan et M' son image par $F$ , l'axe de la similitude est la bissectrice de l'angle $MAM′^\widehat{MAM'}$

Choisis un point $M$ judicieux.
Je te conseille $O (0, 0)$
L'mage $O^{'}$ de $O$ par $F$ est le point d'affixe $2 + i$ c'est à dire le point de coordonnées $(2, 1)$
L'axe de la similitude est la bissectrice de l'angle $OAO′^\widehat{OAO'}$

Fais un schéma, et tu dois trouver sans difficulté que cette droite $(Δ)(\Delta)$ passe passe par le point $B (0, 2)$

Remarque : je l'appelle $B$ car j'imagine que dans l'énoncé $B$ a pour coordonnées (0,2) au lieu de (0,1) mais je l'ignore...
Renomme le si besoin.

L'axe de la similitude est donc la droite $(A B)$

Tu peux déduire que $F$ est le composé commutatif de l'homothétie $H$ de centre A et de rapport $12\dfrac{1}{2}$ avec la réflexion $R$ ( on dit aussi symétrie orthogonale) d'axe (AB)
$F = H o R = R o H$

Avec cela, tu dois pouvoir trouver la seconde question.

Bon travail.

@omah ,

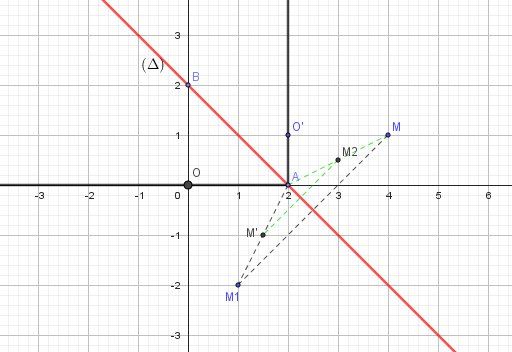
Illustration graphique de cette similitude

$M$ est un point quelconque et $M^{'}$ son image par $F$ (construite des deux façons possibles)