Similitudes suite numerique

[omah]

Bonsoir
Le plan est rapporté à un repère orthonormé (0; u, v). Soit a un réel non nul distinct de 1 et à l'affinité d'axe (D): y$=\frac{1}{1-a}$ de rapport a et de direction définie par v.
)1. Déterminer l'expression analytique de h.
2. On considère la suite des points (Mn)_n appatenant a N définie par M_0(0;2) et quelque soit n appartenant a N , M_n+1= h(M_n). On note $(X_n,Y_n)$ les coordonnees de M_n, dans le repère (0;u;v)

Besoin daide pour la premiere qyestion svp

[omah]

@omah bonsoir aidez moi svp

[mtschoon]

@omah , bonsoir,

Piste

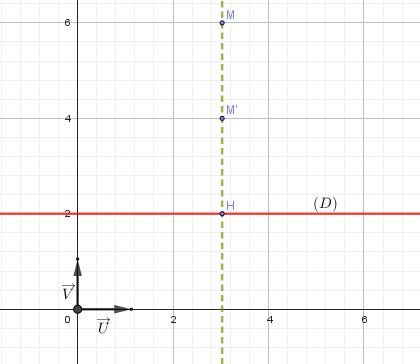
Si j'ai bien lu, l'axe de l'affinité est la droite (D) parallèle à l'axe des abscisses d'équation $y=\frac{1}{1-a}$
La direction est la direction de l'axe de ordonnées
Le rapport est $a$

$\overrightarrow{H{M}^{\prime }}=a\overrightarrow{HM}$ (***)

Tu utilises les coordonnées
$M(x,y)$
$M^{\prime }(x^{\prime },y^{\prime })$
$H(x,\frac{1}{1-a})$

Utilise la formule (***)

L'égalité des abscisses te permet d'écrire :
$x^{\prime }-x=0$
L'égalité des ordonnées te permet d'écrire :
$y^{\prime }-\frac{1}{1-a}=a(y-\frac{1}{1-a})$

Tu isoles $x^{\prime }$ et $y^{\prime }$

[omah]

@mtschoon Merci

[omah]

@mtschoon
a) exprimer X_n+1 et Y_n+1 en fonction de X_n et Y_n
2) demontrer par recurrence que quelque soit n appartient N , $Y_n=$$2a^n+\frac{1-a^n}{1-a}$

[mtschoon]

@omah ,

A la première question, à l'expression analytique de l'affinité, après simplification, tu as dû trouver :
$x^{\prime }=x$
$y^{\prime }=ay+1$

Donc, au a) de la seconde question, tu dois répondre :
$X_{n+1}=X_n$
$Y_{n+1}=a{Y}_n+1$

Je te laisse faire la récurrence demandée au b).