équation trigonométrique symétrique
-
-lala-o dernière édition par

Bonjour, je n'arrive pas à résoudre cet exercice :
sin3(x)+cos3(x)=98sin^3(x)+cos^3(x)=\frac{9}{8}sin3(x)+cos3(x)=89
-
mtschoon dernière édition par mtschoon

@lala-o , bonjour
Une idée à creuser éventuellement,
Soit f(x)=cos3(x)+sin3(x)f(x)=cos^3(x)+sin^3(x)f(x)=cos3(x)+sin3(x)
Soit g(x)=98g(x)=\dfrac{9}{8}g(x)=89Je te joins la représentation graphique
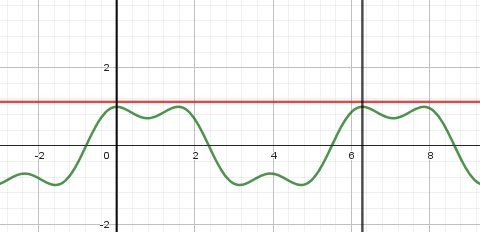
la représentation graphique de fff est en vert
la représentation graphique de ggg est la droite en noirVisiblement, l'équation f(x)=g(x)f(x)=g(x)f(x)=g(x) n' a pas de solution réelle.
Pour le prouver , tu peux étudier les variations de fff sur une période c'est à dire sur [0,2π][0,2\pi][0,2π] par exemple.
(c'est un peu long mais sans difficultés)
Tu dois trouver que le maximum de f(x)f(x)f(x) est 111Vu que 98>1\dfrac{9}{8}\gt 189>1 , l'équation proposée est impossible.
Remarque :
Vu que l'équation est symétrique ( entre sin(x) et cos(x) ) tu peux essayer de la résoudre avec le changement de variable x=y+π4x=y+\dfrac{\pi}{4}x=y+4π
C'est la méthode "classique", mais je n'ai pas essayé...,
-
-lala-o dernière édition par

@mtschoon Bonjour, pouvez vous m'aider pour la méthode du changement de variable? Je vous joint ma résolution pour vous montrer où je bloque.
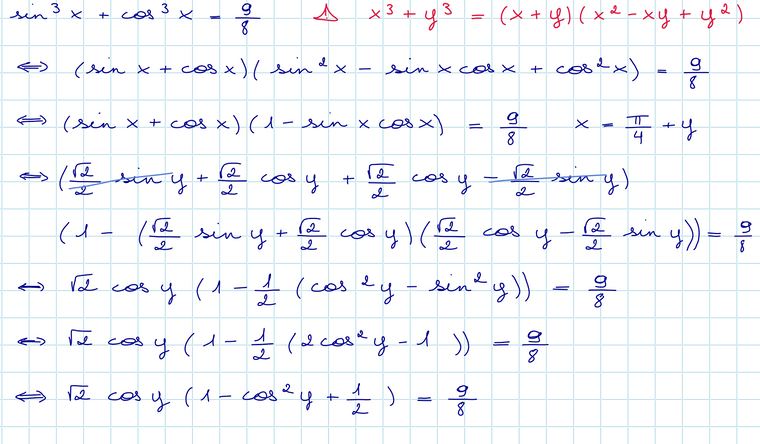
-
BBlack-Jack dernière édition par
Bonjour,
f(x) = sin³(x) + cos³(x)
f '(x) = 3.sin²(x).cos(x) - 3cos²(x).sin(x)
f '(x) = 3.sin(x).cos(x).(sin(x)+cos(x))Etude du signe de f '(x) et f'(x) = 0 ... et on trouve que les extrema de f sont pour x = k.Pi/2 et pour x = Pi/4 + k.Pi
Il suffit donc de calculer ces extrema pour x dans [0 ; 2Pi[ (il n'y en a pas beaucoup)
... et on en déduit que -1 <= f(x) <= 1
--> -1 <= sin³(x) + cos³(x) <= 1
Et donc sin³(x) + cos³(x) = 9/8 n'a pas de solutions.
-
BBlack-Jack dernière édition par Black-Jack
@lala-o a dit dans équation trigonométrique symétrique :
@mtschoon Bonjour, pouvez vous m'aider pour la méthode du changement de variable? Je vous joint ma résolution pour vous montrer où je bloque.
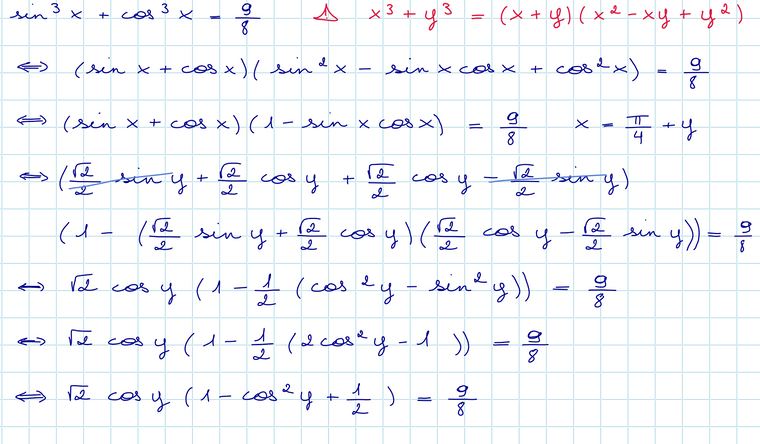
Bonjour,
Je n'ai pas vérifié si c'était correct ...
A supposer que oui.
Il suffit de continuer ainsi : Poser cos(y) = Y
On obtient une équation du 3ème degré en Y :
−2.Y3+322.Y−98=0-\sqrt{2}.Y^3 + \frac{3\sqrt{2}}{2} . Y - \frac{9}{8} = 0−2.Y3+232.Y−89=0Equation facile à résoudre ... et qui donne comme solutions :
a) 2 solutions complexes conjuguées.
b) 1 solution réelle = -1,43...Comme Y = cos(y), on doit forcément avoir -1 <= Y <= 1 ...
et donc aucune des solutions trouvées ne convient.L'équation de départ n'a pas de solutions.
-
mtschoon dernière édition par mtschoon

Bonjour,
@lala-o a dit dans équation trigonométrique symétrique :@mtschoon Bonjour, pouvez vous m'aider pour la méthode du changement de variable? Je vous joint ma résolution pour vous montrer où je bloque.
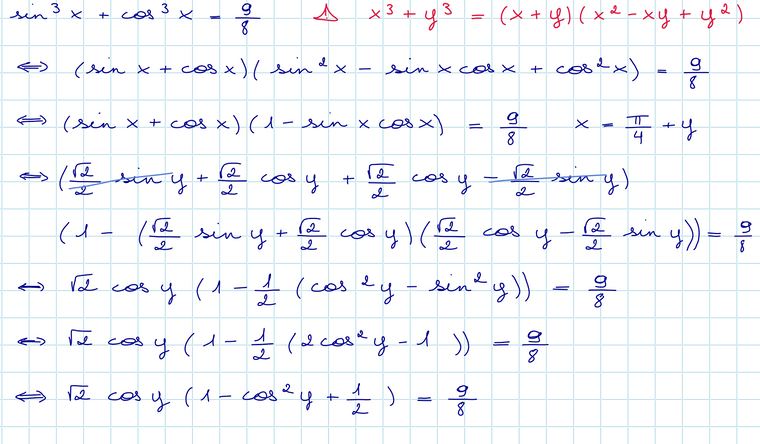
@lala-o , je viens de vérifier tes calculs avec le changement de variable : ils sont corrects.
Bien sûr, tu es obligé(e) de continuer et d'arriver à une équation du 3ème degré sans solution évidente.
Je viens de faire les calculs et trouve la même équation que Black-Jack.
Tu peux éventuellement la transformer pour obtenir une équation de la forme usuelle Y3+pY+q=0\boxed{Y^3+pY+q=0}Y3+pY+q=0:
Y3−32Y+9216=0Y^3-\dfrac{3}{2}Y+\dfrac{9\sqrt 2}{16}=0Y3−23Y+1692=0
Je te mets un lien pour la résolution, si besoin :
https://homeomath2.imingo.net/equa31.htmTu obtiendras la solution réelle en YYY( lourde expression avec des racines cubiques) voisine de −1.4355-1.4355−1.4355, c'est à dire cos(y)≈−1.4355cos(y)\approx-1.4355cos(y)≈−1.4355
D'où impossibilité car tout cosinus est compris entre −1-1−1 et 111
-
mtschoon dernière édition par mtschoon

@lala-o , une remarque.
Tu postes en Terminale(autre) donc on ne peut pas savoir le programme que tu étudies.
Si la résolution des équations du 3ème degré en fait partie, tu peux, comme je te l'ai indiqué, faire le changement de variable x=y+π4x=y+\dfrac{\pi}{4}x=y+4π qui utilise le fait que l'équation proposée est symétrique en sin(x)sin(x)sin(x) et cos(x)cos(x)cos(x).
Sinon, la première méthode que je t'ai proposé en étudiant la fonction fff définie par f(x)=sin3(x)+cos3(x)f(x)=sin^3(x)+cos^3(x)f(x)=sin3(x)+cos3(x) me parait plus simple, mais n'utilise pas la "symétrie" de l'équation.
A toi de voir ce qui correspond le mieux à tes études.
Bon travail.
-
-lala-o dernière édition par

@mtschoon @Black-Jack Merci pour votre aide !
-
mtschoon dernière édition par

De rien @lala-o .
Bon travail !