Géométrie / utilisation de la translation et de la rotation dans une conique
-
Llinjos dernière édition par
Bonjour à tous
Je voudrais obtenir de l'aide pour résoudre cette exercice
En utilisant les translations et les rotations. Trouver pour la conique suivante:
a. La longueur du grand axe
b. La longueur du petit axe
c. La distance focale
d. L'excentricité
e. Le latus rectum
f. Le centre
g. Les sommets
h. Les foyers
i. Les directrices
j. Les asymptotes
k. La polaire du foyer
l. Le cercle orthoptique
Équation de la conique : x²+y²+xy-7x-5y+9=0
Voilà, merci d'avance
-
Llinjos dernière édition par
Ce message a été supprimé !
-
mtschoon dernière édition par mtschoon

@linjos , bonjour,
Pour l'utilisation de la translation et de la rotation dans une conique, je te conseille d'approfondir ce cours ( où tout est expliqué)
https://www.bibmath.net/formulaire/index.php?action=affiche&quoi=coniqueQuelques pistes,
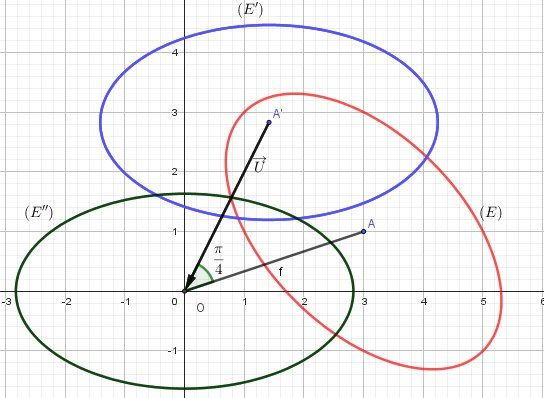
Si j'ai bien lu, tu cherches les caractéristiques le la conique d'équation : x2+y2+xy−7x−5y+9=0\boxed{x^2+y^2+xy-7x-5y+9=0}x2+y2+xy−7x−5y+9=0Avec le déterminant, tu prouves que la conique est une ellipse (E)
Vu que les coefficients de x2x^2x2 et y2y^2y2 sont égaux, tu fais la rotation de centre OOO et d'angle π4\dfrac{\pi}{4}4π
Après calculs, tu dois obtenir, sauf erreur,
x=22x′+22y′x=\dfrac{\sqrt 2}{2}x'+\dfrac{\sqrt 2}{2}y'x=22x′+22y′
y=−22x′+22y′y=\dfrac{-\sqrt 2}{2}x'+\dfrac{\sqrt 2}{2}y'y=2−2x′+22y′
En substituant dans l'équation de (E) tu obtiens l'équation de (E'), image de (E) par cette rotation :
12x′2+32y′2−2x′−62y′+9=0\boxed{\dfrac{1}{2}x'^2+\dfrac{3}{2}y'^2 -\sqrt 2 x'- 6\sqrt 2 y'+9=0}21x′2+23y′2−2x′−62y′+9=0Tu transformes avec les formes canoniques. et tu dois trouver :
12(x′−2)2+32(y′−22)2=4\dfrac{1}{2}(x'-\sqrt 2)^2+\dfrac{3}{2}(y'-2\sqrt 2)^2=421(x′−2)2+23(y′−22)2=4Tu poses :
x′′=x′−2x''=x'-\sqrt 2x′′=x′−2
y′′=y′−22y''=y'-2\sqrt 2y′′=y′−22Par translation de vecteur U→(−2,−22)\overrightarrow{U}(-\sqrt 2, -2\sqrt 2)U(−2,−22), tu obtiens l'équation de l'ellipse (E'') , image de de (E') par cette translation :
12x′′2+32y′′2=4\boxed{\dfrac{1}{2} x''^2+\dfrac{3}{2} y''^2=4}21x′′2+23y′′2=4
Tu pourras encore transformer cette écriture pour l'obtenir sous la forme x′′2a2+y′′2b2=1\dfrac{x''^2}{a^2}+\dfrac{y''^2}{b^2}=1a2x′′2+b2y′′2=1Lorsque tu auras fait tout cela, tu pourras trouver les éléments caractéristiques demandés.
Il y a du travail dans cet exercice !
-
mtschoon dernière édition par mtschoon

@linjos , illustration graphique
-
Llinjos dernière édition par
@mtschoon merci beaucoup !
Oui y a beaucoup à faire, j'espère que ça ira .
-
mtschoon dernière édition par mtschoon

Oui, @linjos , tu as de quoi faire...
Si ça peut t'avancer un peu, je t'indique la formule usuelle de (E'')
x′′2(22)2+y′′2(263)2=1\boxed{\dfrac{x''^2}{\biggr(\dfrac{\sqrt 2}{2}\biggr)^2}+\dfrac{y''^2}{\biggr(\dfrac{2\sqrt 6}{3}\biggr)^2}=1}(22)2x′′2+(326)2y′′2=1
Bon courage pour toutes les caractéristiques.
Remarque : dans les pistes , je n'ai pas changé de repère, j'ai gardé le repère et j'ai trouvé les images de (E) par rotation puis par translation pour trouver une ellipse (E'') isométrique à (E) et de position usuelle.
Tu peux aussi, si tu préfères, garder (E) et faire des changements d'axes par rotation et translation