Probabilités supérieure

Bonjour/Bonsoir j'espère que vous allez bien, j'aimerais avoir besoin d'aide de votre part pour mon DM que je bloque dessus.
On étudie la cote X d'une pièce produite par une machine. On suppose que X suit une loi normale de moyenne m = 20 mm et d'écart-type σ = 0.26 mm.
1º) La cote est considérée correcte si m - 3σ ≤ X ≤ m + 3σ. Calculer la probabilité que la cote soit correcte.
2°) Déterminer a tel que p[ X ≤ a ] soit égale à 20%. Interpréter ce résultat.
3°) Les pièces produites sont classées en premier choix et en second choix. On prélève au hasard un échantillon de 400 pièces dans lequel on observe 120 pièces de premier choix.
Déterminer, au risque de 4%, un intervalle où se situe la proportion des pièces de premier choix dans la production.
4°) Une autre cote Y suit une loi normale d'écart-type 0,20 mm. On veut que cette cote soit de 25 mm. On prélève au hasard un échantillon de 40 pièces et on observe sur cet échantillon une moyenne de 24,90 mm.
a) Peut-on dire, au seuil de 4%, que la machine est bien réglée? Expliquer.
b) Qu'entend-on par risque de première espèce? Risque de deuxième espèce? Quel risque court-on avec votre réponse au a)? Expliquer.
c) Calculer le risque de deuxième espèce correspondant à la zone d'acceptation au risque de 4% déterminée à la question a).
5°) Sur une autre machine, on étudie une cote Z qui suit une loi normale d'écart-type inceanu. La valeur correcte de cette cote 25 mm.On prélève au hasard un échantillon de 9 pièces et on obtient, en mm les cotes suivantes: 24,53 - 25, 23 - 24, 97 - 24, 82 - 24, 84 - 25, 21 - 25, 10 - 25, 29 - 25,24.
a) Calculer, en justifiant, une estimation de l'écart-type.
b) Peut-on dire, au seuil de 5%, que 2010 le réglage de la machine est correct? Expliquer.

@medou-coulibaly Bonjour,

Indique tes éléments de réponse et la question qui te pose problème

Calcule : $P(20−3×0,26≤X≤20+3×0,26)P(20-3\times0,26 \leq X \leq 20+3\times0,26)$

@Noemi Bonsoir Néomi je comprends pas votre question

@Noemi quqnd je calcule je trouve ceci P ( 4,42 ≤ X ≤ 5,98 )

@medou-coulibaly

Il n'y a pas de parenthèse entre $20 - 3$
Calcule la probabilité $\leq X\leq 20,78)$

@Noemi bonjour monsieur,et la deuxième question monsieur comment en abord

@Donassi-soungari-Soro

Tu as trouvé combien à la première question ?

@Noemi nous sommes là en même temps monsieur

@Noemi 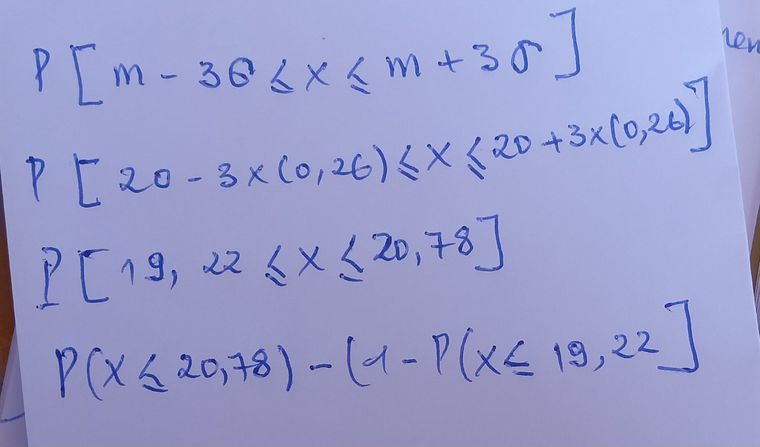nous sommes passés par cette méthode

@Noemi pour la probabilité P (T≤ 20,78 ) = 0,99865 c'est ce qu'on trouve

@Noemi pour la P[T≤ 19,22 ]= 0,99865

@Noemi P[ 19,22 ≤ x ≤ 20,78 ] = 0,9973
C'est ce qu'on trouve comme probabilité correcte