Application affine , dans le plan urgent

Bonsoir
Le plan est muni d'un repère orthonormé (0; i; J) dans lequel on considère les points
A(0;2); B(0; 1); C(1; 1); D(1; 2)et E(2; 1)
Soit f l'application affine du plan qui transforme le point O en A et dont l'application linéaire associée est notée $ϕ\phi$
On suppose que pour tout point M de la droite (BC), on a $V e c M f (M) = v e c j$

a) Déterminer f(B) et f(C)
b) Déterminer la matrice de ‹ dans la base (I;j)
Soit M un point du plan de coordonnées (x, y) dans le repère(0;i;j). Démontrer que
$\vecMf(M) = (2 - y)j
Démontrer que fof = f. En déduire la nature et les éléments caractéristiques de f.
aidez moi svp

@MMounah bonsoir
@Black-Jack @mtschoon

@MMounah , bonjour,

Quelques pistes à creuser,

Schéma
Notation : $M^{'} = f (M)$
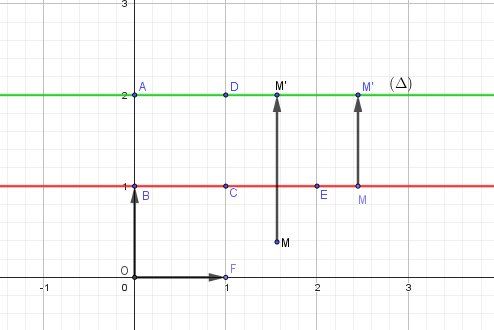
Affinité.jpg

1 ) En utilisant les hypothèses, tu peux déduire :
$f (O) = A$
$f (B) = A$
$f (C) = D$

Soit m la matrice de $Φ\Phi$

Tu dois trouver $Φ(i→)\Phi(\overrightarrow{i})$ et $Φ(j→)\Phi(\overrightarrow{j})$

$Φ(i→)=Φ(BC→)=f(B)f(C→)=AD→\Phi(\overrightarrow{i})=\Phi(\overrightarrow{BC})=\overrightarrow{f(B)f(C})=\overrightarrow{AD}$
$Φ(j→)=Φ(OB→)=f(O)f(B→)=AA→=0→\Phi(\overrightarrow{j})=\Phi(\overrightarrow{OB})=\overrightarrow{f(O)f(B})=\overrightarrow{AA}=\overrightarrow{0}$

D'où $0)m=\begin{pmatrix}1 \ \ 0\cr 0\ \ 0\end{pmatrix}$

2 ) $M (x, y)$
$f(M)=f(O)+Φ(OM→)=A+Φ(OM→)f(M)=f(O)+\Phi(\overrightarrow{OM})=A+\Phi(\overrightarrow{OM})$

Tu dois trouver : $f (M)$ pour coordonnées $(x, 2)$

Puis $Mf(M)→\overrightarrow{Mf(M)}$ a pour coordonnées $(0, 2 - y)$ d'où la réponse proposée

3 ) $M$ a pour coordonnées $(x, y)$
$f (M)$ a pour coordonnées $(x, 2)$
$f (f (M))$ a pour coordonnées $(x, 2)$
d'où $f o f = f$

Tu dois déduire que $f$ est la projection orthogonale sur la droite $(Δ)(\Delta)$ d'équation $y = 2$

Tout ceci est à détailler avec soin.
Bon travail.

@MMounah , si tu as besoin de détails sur les applications affines, tu peux consulter éventuellement ici :https://webusers.imj-prg.fr/~christian.blanchet/enseignement/2013-14/L3/ch2_appl_affines.pdf

@mtschoon bonsoir
Madame j’ai pas bien compris la question 2.

@MMounah , bonjour,

J'explicite un peu la question 2)

J'utilise les notations du lien que je t'ai donné.
Adapte si besoin.

$f(M)=f(O)+Φ(OM→)f(M)=f(O)+\Phi(\overrightarrow{OM})$

$f(O)=A=(02)f(O)=A=\begin{pmatrix}0\cr 2\end{pmatrix}$
$OM→=(xy)\overrightarrow{OM}=\begin{pmatrix}x\cr y\end{pmatrix}$

$m$ étant matrice de $Φ\Phi$ calaculée précédemment

$Φ(OM→)=m×(xy)\Phi(\overrightarrow{OM})=m\times \begin{pmatrix}x\cr y\end{pmatrix}$

$Φ(OM→)\Phi(\overrightarrow{OM})$ = $0)×(xy)=(x0)\begin{pmatrix}0 \ \ 1\cr 0\ \ 0\end{pmatrix} \times \begin{pmatrix}x\cr y\end{pmatrix}=\begin{pmatrix}x\cr 0\end{pmatrix}$

Donc

$f(M)=(02)+(x0)=(x2)f(M)=\begin{pmatrix}0\cr 2\end{pmatrix}+\begin{pmatrix}x\cr 0\end{pmatrix}=\begin{pmatrix}x\cr 2\end{pmatrix}$

Conséquence :
$Mf(M)→=(x2)−(xy)=(x−x2−y)=(02−y)\overrightarrow{Mf(M)}=\begin{pmatrix}x\cr 2\end{pmatrix}-\begin{pmatrix}x\cr y\end{pmatrix}=\begin{pmatrix}x-x\cr 2-y\end{pmatrix}=\begin{pmatrix}0\cr 2-y\end{pmatrix}$

Tu tires la conclusion.