3. nombre complexe exercice

nombre complexe exercice

  • J

    boujour j'ai un exercice où je ne comprends pas la dernière question.
    on considère le polynôme P de la variable complexe défini par P(Z)=Z⁴+Z³-Z-1

    1. montre P(Z) se met sous la forme P(Z)=(Z-1)Q(Z) où Q(Z) est un polynôme à déterminer
    2. écrit Q(Z) sous la forme Q(Z)=(Z+1)R(Z)
      où R(Z) est un polynôme à déterminer
    3. résous dans l'ensemble C l'équation P(Z)=0
    4. la solution de la partie imaginaire strictement positif. calculer( alpha)²(alpha)³(alpha)⁴(alpha)⁵(alpha)⁶ puis calculer (alpha)²⁰⁰⁴
      réponse
    5. pour cette question comme P(-1)=0 alors P(
      Z)=(Z-1)Q(Z) avec Q(Z) un polynôme de degrés 3 tel que Q(Z)=aZ³+bZ²+CZ+d en développant et en utilisant la méthode par identification je trouve Q(Z)=Z³+1
    6. j'ai appliqué la même démarche dans la question précédente et j'ai trouvé R(Z)=Z²-Z+1
    7. pour la question 3 on P(Z)=(Z-1)(Z+1)(Z²-Z+1)=0 donc les solutions sont {-1;1;1/2+√(3)i/2;1/2-√(3)i/2}
      c'est au niveau de la dernière question que je n'arrive pas à comprendre.
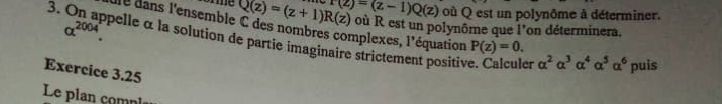
      1715480809887.jpg
  • W

    Bonjour jean 12

    quelle est la dernière question? le point 3. de ta copie?

    J 1 réponse
  • B

    Bonjour,

    De nos jours, on a l'art de tout compliquer...

    Je le fais à ma façon :

    Z4+Z3−Z−1=0Z^4 + Z^3 - Z - 1 = 0Z4+Z3−Z−1=0
    Z3(Z+1)−(Z+1)=0Z^3(Z+1)-(Z+1)=0Z3(Z+1)−(Z+1)=0
    (Z+1)(Z3−1)=0(Z+1)(Z^3-1)= 0(Z+1)(Z3−1)=0
    (Z+1)(Z−1)(Z2+Z+1)=0(Z+1)(Z-1)(Z^2+Z+1)=0(Z+1)(Z−1)(Z2+Z+1)=0 (identité remarquable qui devrait être connue depuis la Seconde)

    Z2+Z+1=0Z^2+Z+1 = 0Z2+Z+1=0
    Z=−1±i.32Z = \frac{-1\pm i.\sqrt{3}}{2}Z=2−1±i.3​​

    S={−1,1,−1−i.32,−1+i.32}S= \{-1 , 1 , \frac{-1-i.\sqrt{3}}{2} , \frac{-1+i.\sqrt{3}}{2} \}S={−1,1,2−1−i.3​​,2−1+i.3​​}

    On a donc α=−1+i.32\alpha = \frac{-1+i.\sqrt{3}}{2}α=2−1+i.3​​

    On calcule α2=−1−i.32\alpha^2 = \frac{-1-i.\sqrt{3}}{2}α2=2−1−i.3​​

    On calcule α3=1\alpha^3 = 1α3=1

    On calcule α4=−1+i.32=α\alpha^4 = \frac{-1+i.\sqrt{3}}{2} = \alphaα4=2−1+i.3​​=α

    Donc α1+3n=α\alpha^{1 + 3n} = \alphaα1+3n=α (avec n dans N)
    et α3n=1\alpha^{3n} = 1α3n=1

    Comme 2004 = 3 * 668, α2004\alpha^{2004}α2004 est de la forme α3n\alpha^{3n}α3n ...

    Et donc α2004=1\alpha^{2004} = 1α2004=1

    J 1 réponse
  • W

    @Black-Jack

    sans doute une petite erreur de recopie ici (Z+1)(Z+1)(Z2+Z+1)=0(Z+1)(Z+1)(Z^2+Z+1)=0(Z+1)(Z+1)(Z2+Z+1)=0 , mais qui est corrigée ensuite

    personnellement, j'ai utilisé une variante qui consiste à passer par la forme exponentielle du nombre complexe, mais comme souvent, il n'y a pas qu'une seule méthode de résolution

  • J

    @Black-Jack bonjour
    je n'arrive pas à comprendre ce que vous avez faire. j'ai du mal aussi à bien comprendre la dernière question si vous pouvez clairement m'expliquer afin que je puisse comprendre

  • J

    @Wilmat bonjour
    oui c'est la dernière question

  • W

    @jean-12 a dit dans nombre complexe exercice :

    @Wilmat bonjour
    oui c'est la dernière question

    @jean-12
    je laisserai @Black-Jack répondre puisqu'il a presque tout dit

    J 1 réponse
  • J

    @Wilmat bonjour
    d'accord.

  • B

    Bonjour,

    J'ai corrigé l'erreur de frappe de ma première réponse ... (conformément à la remarque de Wilmat 🙂 )

    La solution complexe de P(Z) = 0 qui a sa partie réelle positive est α=−1+i.32\alpha = \frac{-1+i.\sqrt{3}}{2}α=2−1+i.3​​

    On calcule alors α2\alpha^2α2 et α3\alpha^3α3 et α4\alpha^4α4... et avec ces résultats, on peut conclure que αk=1\alpha^k = 1αk=1 si k = 3.n (avec n compris dans N). (Faire l'effort de réflexion qui permet cette conclusion).

    Comme 2004 est un multiple de 3 ... on sait alors que α2004=1\alpha^{2004} = 1α2004=1

Se connecter pour répondre