Géométrie des courbes et de surfaces
-
medou coulibaly dernière édition par medou coulibaly

Bonjour comment vous allez, j'ai besoin d'aide pour mon DM.
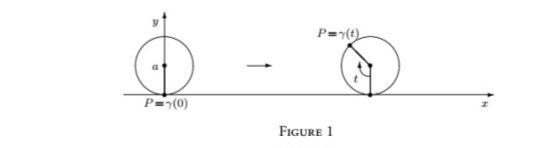
Dans un plan vertical , un disque de rayon a > 0 roule sans glisser sur une droite horizontale. La courbe tracée par un point P fixé au bord du disque s'appelle cycloïde.- Donner un paramétrage γ ( t ) de la cycloïde, en prenant comme paramètre t l'angle compris entre le rayon du disque passant par P à l'instant 0 et celui à l'instant t, comme dans la figure 1.
- Dessiner la cycloïde pour t ∈ [- pi; 5pi ]
- Calculer l'abscisse curviligne s(t).
- Calculer la longueur d'arc de la cycloïde après un tour complet du disque.
- Calculer la courbure de la cycloïde paramétrée par γ.
-
BBlack-Jack dernière édition par
Bonjour,
x(t) = a*(t - sin(t))
y(t) = a*(1-cos(t))avec t en radians
Attention,
Il peut y avoir ergotage sur le signe de t.
Si on prend les conventions les plus souvent utilisées, l'angle t est négatif quand le mobile se déplace vers la droite, mais ce n'est probablement pas la convention de l'auteur de la question (va savoir ?)....
-
medou coulibaly dernière édition par

@Black-Jack
Bonjour monsieur, merci pour votre réponse mais le prof n'a pas donné plus précision sur la question.
Pour cette question est-ce qu'on peut se limiter là ?
-
BBlack-Jack dernière édition par
@medou-coulibaly a dit dans Géométrie des courbes et de surfaces :
@Black-Jack
Bonjour monsieur, merci pour votre réponse mais le prof n'a pas donné plus précision sur la question.
Pour cette question est-ce qu'on peut se limiter là ?J'ai donné les équations demandées (à la réserve du signe de t près déjà mentionnée)
Tu peux compléter en démontrant ces formules ... Cela est presque immédiat.Quand la roue tourne de l'angle t, son centre avance vers la droite d'une distance at
Le point P est à une distance horizontale du centre d'une longueur -a.sin(t) (dessiner le triangle adéquat sur la roue pour le démontrer)
... Et donc x(t) = at - a.sin(t) = a(t-sint(t))Avec le même triangle que celui mentionné ci dessus, on montre que : y = a - a.cos(t) = a(1-cos(t))
-
medou coulibaly dernière édition par

@Black-Jack j'ai essayé de démontrer mais je n'arrive pas à trouver
-
@medou-coulibaly Bonjour,
Consulte ce cours : https://www.deleze.name/marcel/sec2/cours/CalculIntegral/cycloide.pdf
-
medou coulibaly dernière édition par

@Noemi Bonjour monsieur , j'ai consulté votre lien envoyé mais je n'arrive pas à bien distinguer mes questions.
Pouvez m'éclaircir..
-
Le début est la démonstration pour le paramétrage de la cycloïde, puis tu as la démonstration pour la longueur de l'arc.
-
medou coulibaly dernière édition par

@Noemi et la qu'est 2 et 3 ?
-
La question 2 est le tracé de la cycloïde, utilise le cours pour la représentation graphique d'une courbe paramètre.
Pour la question 3, quelle est la relation pour l'abscisse curviligne ?
-
medou coulibaly dernière édition par

@Noemi j'ai sérieusement besoin d'aide pour la 3 car j'ai pas trop de connaissance la dessus
-
L'abscisse curviligne est une primitive de : x′(t)2+y′(t)2\sqrt{x'(t)^2+y'(t)^2}x′(t)2+y′(t)2
-
medou coulibaly dernière édition par

@Noemi ok d'accord je vais essayer et vous revenir