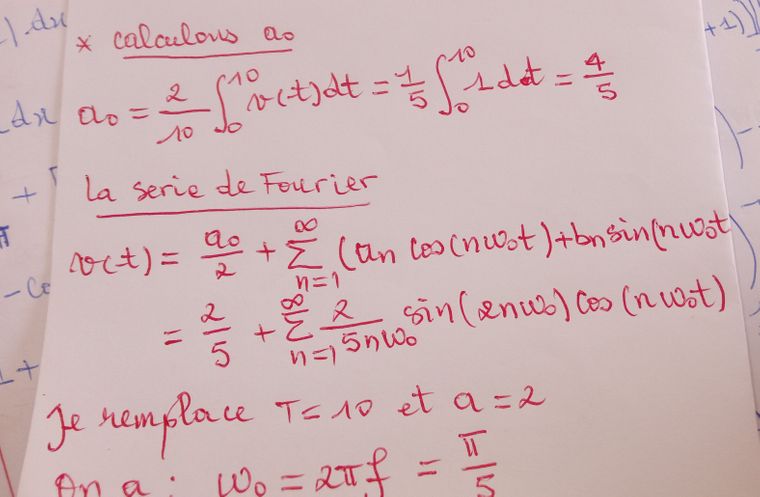Transformée de Fourier : Série de Fourier
-
medou coulibaly dernière édition par medou coulibaly

J'ai besoin d'aide.
Trouver la FS pour un train d'impulsions périodique défini sur une période comme :
r(t) = 1for|t| < a; 0fora < |t| < T/2
En déduire le FS avec T = 10 a = 2
-
@medou-coulibaly Bonjour,
Il serait bien de comprendre les autres exercices avant d'en proposer d'autres.
Vérifie l'énoncé.Pour déterminer la série de Fourier (FS) d'un train d'impulsions périodique défini par :
r(t)={1 pour ∣t∣<a0 pour a<∣t∣<T/2r(t) =\begin{dcases}1 \ \text{pour } |t| \lt a \cr 0 \ \text{pour } a \lt |t| \lt T/2 \end{dcases} r(t)={1 pour ∣t∣<a0 pour a<∣t∣<T/2Les coefficients de la série de Fourier pour un signal périodique sont donnés par :
a0=1T∫0Tr(t) dta_0 = \dfrac{1}{T} \int_{0}^{T} r(t) \ dta0=T1∫0Tr(t) dtLes coefficients ana_nan et bnb_nbn sont donnés par :
an=2T∫0Tr(t)cos(2πntT) dta_n = \dfrac{2}{T} \int_{0}^{T} r(t) \cos\left(\dfrac{2\pi nt}{T}\right) \ dtan=T2∫0Tr(t)cos(T2πnt) dt
bn=2T∫0Tr(t)sin(2πntT) dtb_n = \dfrac{2}{T} \int_{0}^{T} r(t) \sin\left(\dfrac{2\pi nt}{T}\right) \ dtbn=T2∫0Tr(t)sin(T2πnt) dt
Indique tes calculs et/ou résultats si tu souhaites une vérification.
-
r(t)r(t)r(t) est une impulsion de durée 2a2a2a qui se répète toutes les TTT secondes.
La série de Fourier d'un signal périodique r(t)r(t)r(t) est donnée par :
r(t)=∑n=−∞+∞cnej2πnTtr(t) = \sum_{n=-\infty}^{+\infty} c_n e^{j \frac{2\pi n}{T} t}r(t)=∑n=−∞+∞cnejT2πnt
où cnc_ncn sont les coefficient de Fourier donné par :cn=1T∫0Tr(t)e−j2πnTtdtc_n = \frac{1}{T} \int_{0}^{T} r(t) e^{-j \frac{2\pi n}{T} t} dtcn=T1∫0Tr(t)e−jT2πntdt
Ici l'intégrale se limite à l'intervalle où r(t)=1r(t) = 1r(t)=1, c'est-à-dire de −a-a−a à aaa. Donc,
cn=1T∫−aa1⋅e−j2πnTtdtc_n = \frac{1}{T} \int_{-a}^{a} 1 \cdot e^{-j \frac{2\pi n}{T} t} dtcn=T1∫−aa1⋅e−jT2πntdt
Soit :
cn=1T[e−j2πnTt−j2πnT]−aa=1T(e−j2πnTa−ej2πnTa−j2πnT)c_n = \frac{1}{T} \left[ \frac{e^{-j \frac{2\pi n}{T} t}}{-j \frac{2\pi n}{T}} \right]_{-a}^{a} = \frac{1}{T} \left( \frac{e^{-j \frac{2\pi n}{T} a} - e^{j \frac{2\pi n}{T} a}}{-j \frac{2\pi n}{T}} \right)cn=T1[−jT2πne−jT2πnt]−aa=T1(−jT2πne−jT2πna−ejT2πna)
En simplifiant,
cn=1T⋅2jsin(2πnaT)−j2πnT=1πnsin(2πnaT)c_n = \frac{1}{T} \cdot \frac{2j \sin\left(\frac{2\pi n a}{T}\right)}{-j \frac{2\pi n}{T}} = \frac{1}{\pi n} \sin\left(\frac{2\pi n a}{T}\right)cn=T1⋅−jT2πn2jsin(T2πna)=πn1sin(T2πna)Je te laisse poursuivre. Indique tes calculs et/ou résultat si tu souhaites une vérification.
-
medou coulibaly dernière édition par

@Noemi je trouve d'abord
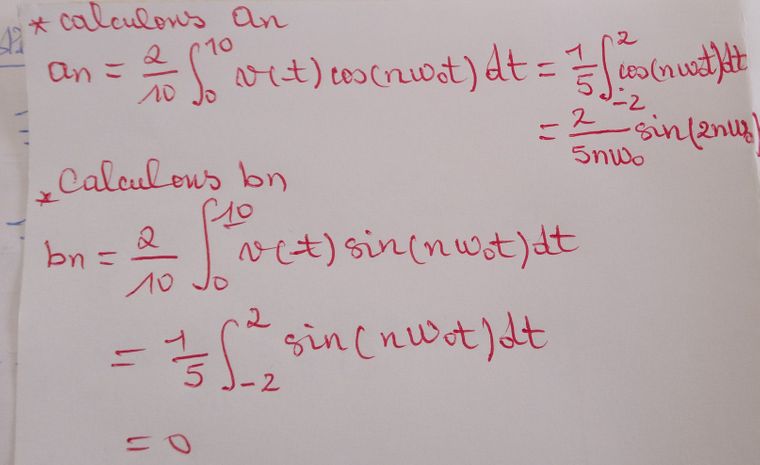
-
medou coulibaly dernière édition par

-
medou coulibaly dernière édition par

-
medou coulibaly dernière édition par

@medou-coulibaly
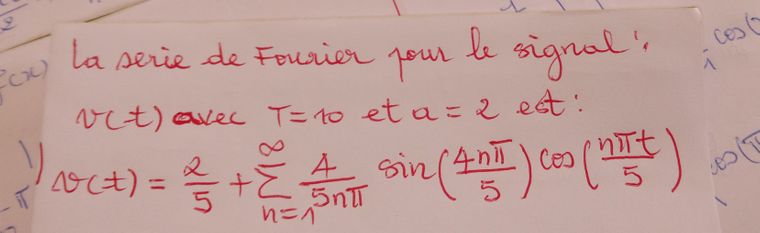 

-
Vérifie tes calculs;
-
medou coulibaly dernière édition par

@Noemi ok d'accord

-
medou coulibaly dernière édition par

@Noemi Bonjour j'ai eu un souci avec mon compte.
C'est maintenant que j'arrive à me connecter