Bloqué sur une limite de suite

Bonjour,
Je me permets de poster ce message car j’ai besoin d’aide pour une question sur la quelle je bloque. Je dois trouver la limite éventuelle de la suite en photo en dessous. Et pour montrer que celle ci diverge sans limite j’ai comme piste d’utiliser des suites extraites mais les seules que je trouve nécessitent des parties entières (fonctions des suites extraites en photo en dessous aussi) ce qui pose problème pour la simplification qui est impossible ensuite.
Auriez vous une idée pour que je puisse me débloquer ?
Merci d’avance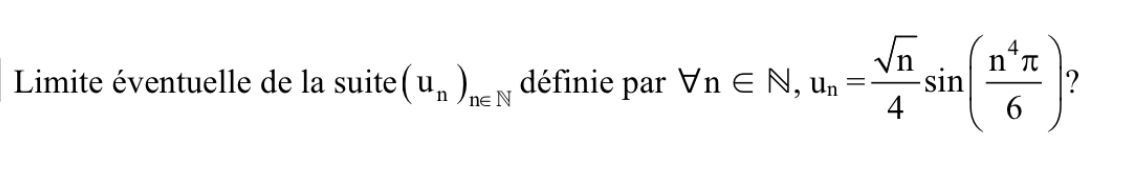

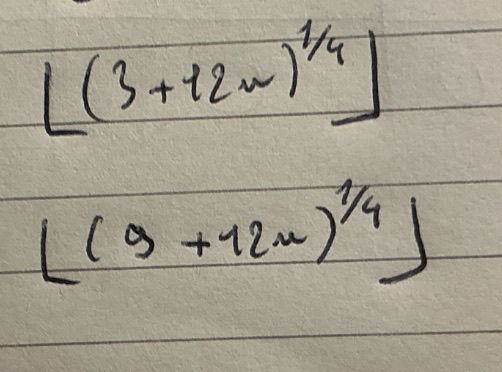
@jules_bkz Bonsoir,

Soit la suite $U_n$ définie par
$Un=n4sin⁡(n4π6)U_n = \dfrac{\sqrt{n}}{4} \sin\left(\dfrac{n^4 \pi}{6}\right)$ ,

Tu indiques que lorsque $n$ augmente, $n\sqrt{n}$ tend vers l'infini.

La fonction sinus oscille entre $- 1$ et $1$ quel que soit $n$ . Par conséquent, $sin⁡(n4π6)\sin\left(\dfrac{n^4 \pi}{6}\right)$ ) ne converge pas vers une valeur spécifique, mais reste bornée.

Bilan
La suite $U_n)$ ne converge pas vers une limite spécifique. La suite, $U_n)$ va osciller entre des valeurs de plus en plus grandes (en valeur absolue) à mesure que $n$ augmente.

Donc la suite $U_n)$ ne possède pas de limite.

D’accord merci beaucoup pour votre réponse

@jules_bkz

Parfait, si tu as compris la démonstration.