généralités sur les signaux
-
Jjean 12 dernière édition par
bonsoir j'ai un exercice sur les signaux et j'aimerais avoir votre aide afin de comprendre l'exercice.
f(t)=2r(t-5)-r(t-10)-r(t-15)
où r(t) est un échelon de vitesse unitaire.
complétez le tableau puis tracez le graphe de f(t).
comme r(t) est un échelon de vitesse unitaire alors r(t)={0 pour t<0 et t pour t>0
maintenant pour compléter le tableau je ne sais pas si je dois remplacer les différentes valeurs par t mais dans ce cas je n'arrive pas trouver quelque chose parce que je ne comprends même pas cette partie.
-
@jean-12 Bonjour,
Vérifie l'énoncé, l'échelon de vitesse est-il défini par :
r(t)={0 si t<01 si t≥0r(t) =\begin{cases} 0 \ \text{si } t \lt 0 \cr 1 \ \text{si } t \geq 0\end{cases}r(t)={0 si t<01 si t≥0 ?sachant que :
f(t)=2r(t−5)−r(t−10)−r(t−15)f(t) = 2r(t-5) - r(t-10) - r(t-15)f(t)=2r(t−5)−r(t−10)−r(t−15)
Calcul de f(0)f(0)f(0) :
f(0)=2r(0−5)−r(0−10)−r(0−15)=2r(−5)−r(−10)−r(−15)=2×0−0−0=0f(0) = 2r(0-5) - r(0-10) - r(0-15) = 2r(-5) - r(-10) - r(-15) = 2 \times 0 - 0 - 0 = 0f(0)=2r(0−5)−r(0−10)−r(0−15)=2r(−5)−r(−10)−r(−15)=2×0−0−0=0
Calcul de f(5)f(5)f(5)
f(5)=2r(5−5)−r(5−10)−r(5−15)=2r(0)−r(−5)−r(−10)=2×1−0−0=2f(5) = 2r(5-5) - r(5-10) - r(5-15) = 2r(0) - r(-5) - r(-10) = 2 \times 1 - 0 - 0 = 2f(5)=2r(5−5)−r(5−10)−r(5−15)=2r(0)−r(−5)−r(−10)=2×1−0−0=2Je te laisse poursuivre. indique tes calculs et/ou résultats si tu souhaites une vérification.
-
BBlack-Jack dernière édition par
Bonjour,
Il ne faut pas confondre "l'échelon unitaire" appelé aussi par les physiciens "échelon unitaire de position" avec l'"échelon unitaire de vitesse"
Pour moi (mais aller vérifier la définition dans le cours, car elle pourrait bien différer d'un prof à l'autre), l'échelon de vitesse unitaire r(t) est tel que :
r(t) = 0 pour t < 0
r(t) = t pour t >= 0Pour t < 0, f(t) = 0
Pour t >=0, f(t) = 2t.(t-5) - t.(t-10) - t.(t - 15)
Pour t >=0, f(t) = t.(2t-10 - t+10 -t + 15)
Pour t >=0, f(t) = 15tEx f(5) = 15*5 = 75
-
Jjean 12 dernière édition par
@Black-Jack bonsoir
j'aimerais savoir pourquoi vous avez remplacez les r par t vue que le r est une fonction mais je n'arrive pas à comprendre pourquoi vous avez remplacez par t. merci d'avance
-
Si la fonction rrr est-elle bien définie par :
r(t)={0 si t<0t si t≥0r(t) =\begin{cases} 0 \ \text{si } t \lt 0 \cr t \ \text{si } t \geq 0\end{cases}r(t)={0 si t<0t si t≥0dans ce cas : f(0)=f(5)=0f(0)=f(5)=0f(0)=f(5)=0
f(10)=10f(10)=10f(10)=10
f(15)=f(100)=...=15f(15)=f(100)=... = 15f(15)=f(100)=...=15Tu peux ensuite tracer le graphe.
-
Jjean 12 dernière édition par
@Noemi bonjour
j'aimerais juste savoir comment le calcul de fait j'aimerais connaître la logique
-
Tu appliques la relation de la fonction fff en utilisant la définition de la fonction rrr.
Soit : f(t)=2r(t−5)−r(t−10)−r(t−15)f(t)=2r(t-5)-r(t-10)-r(t-15)f(t)=2r(t−5)−r(t−10)−r(t−15)
Si t=0t=0t=0 : f(0)=2r(0−5)−r(0−10)−r(0−15)f(0)=2r(0-5)-r(0-10)-r(0-15)f(0)=2r(0−5)−r(0−10)−r(0−15)
Soit f(0)=2r(−5)−r(−10)−r(−15)f(0)=2r(-5)-r(-10)-r(-15)f(0)=2r(−5)−r(−10)−r(−15)
donc f(0)=2×0−0−0=0f(0)=2\times 0 - 0 - 0= 0f(0)=2×0−0−0=0Si t=10t=10t=10 : f(10)=2r(10−5)−r(10−10)−r(10−15)f(10)=2r(10-5)-r(10-10)-r(10-15)f(10)=2r(10−5)−r(10−10)−r(10−15)
f(10)=2r(5)−r(0)−r(−5)f(10)=2r(5)-r(0)-r(-5)f(10)=2r(5)−r(0)−r(−5)
f(10)=2×5−0−0=10f(10)=2\times5-0-0=10f(10)=2×5−0−0=10Je te laisse vérifier les autres.
-
Jjean 12 dernière édition par
@Noemi bonjour
j'ai calculé et j'ai trouvé maintenant
f(15)=2r(10)-r(5)-r(0)=15
f(100)=2r(95)-r(90)-r(85)=15
f(1000)=2r(950)-r(900)-r(850)=15
maintenant pour la construction on peut dire que f(t)=0 si t<=5, f(t)=10 si t=10 et f(t)=15 si t>=15
-
C'est correct, tu peux tracer le graphe.
-
Jjean 12 dernière édition par
@Noemi
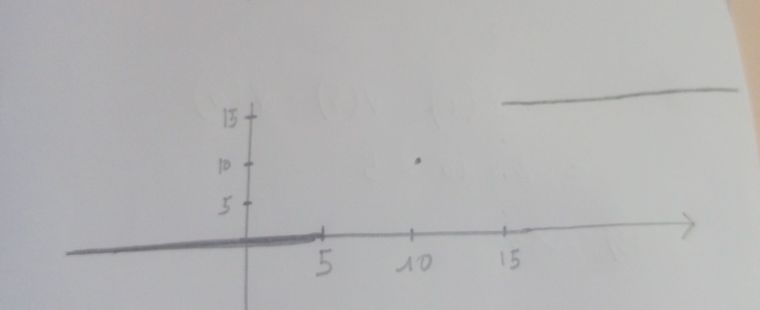 voici le graphe
voici le graphe
-
Il faut représenter la partie entre 555 et 151515.
Soit à tracer le segment qui va du point de coordonnées (5;0)(5;0)(5;0) au point de coordonnées (10;10)(10;10)(10;10) puis du point de coordonnées (10;10)(10;10)(10;10) au point de coordonnées (15;15)(15;15)(15;15). Expression des fonctions correspondant au segment à préciser.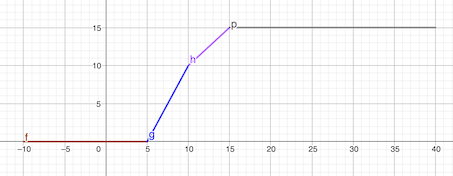
-
BBlack-Jack dernière édition par
J'avais, à tort, lu :
f(t) = 2r(t).(t-5) - r(t).(t-10) - r(t).(t-15)
... d'où ma réponse précédente.