exercic outil maths pour signal

bonsoir j'ai un exercice et j'aimerais avoir de l'aide pour pouvoir avancer.
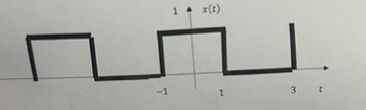
Voici l'énoncé de l'Exercice 1 :

On considère le signal , périodique, défini par le graphe suivant :

Calculer la valeur moyenne et la valeur efficace du signal
Calculer l’amplitude du fondamental de .
pour la valeur moyenne vue que le Signal est un signal en crainaau alors la valeur moyenne est nul est la valeur efficace est égal à 1
au niveau de la deuxième question je sais que je dois d'abord déterminer les coefficients de Fourier pour pouvoir déterminer le fondamentale mais je n'arrive pas à déterminer l'expression du signal
merci d'avance

@jean-12 Bonjour,

$x (t) = 1$ pour $−T4<t<T4-\dfrac{T}{4} \lt t \lt \dfrac{T}{4}$

$x (t) = 0$ pour $T4<t<3T4\dfrac{T}{4} \lt t \lt \dfrac{3T}{4}$

Bonjour,

Tu fais beaucoup d'erreurs.

La valeur moyenne est 1/2 et certainement pas 0.
Ce serait 0 si le signal était symétrique par rapport à l'axe des abscisses (le temps), mais ce n'est évidemment pas le cas ici.

$xˉ=∫−111.dt+∫130.dt4=12\bar{x} = \frac{\int_{-1}^1 1.dt + \int_{1}^{3} 0.dt}{4} = \frac{1}{2}$

Erreur également dans la valeur efficace ... qui ici se calcule par :
$1T.∫0T2.12dt\sqrt{\frac{1}{T}.\int_0^{\frac{T}{2}}.1^2 dt}$ ... on arrive alors à $12\sqrt{\frac{1}{2}}$

Après avoir (vraiment) compris cela, tu devrais pouvoir continuer.

@Noemi bonjour
comment vous avez fait pour déterminer les expressions pouvez vous m'expliquer svp

@Black-Jack bonjour
vue qu'on avait fait un exemple à peu près semblable je pensais que c'était la même chose merci beaucoup pour votre explication.

Ce message a été supprimé !

@jean-12

Pour déterminer les expressions, tu détermines en premier la période, ici $T = 4$ , tu choisis ensuite sur le signal une période et tu analyses la courbe.
J'ai choisis une période allant de $- 1$ à $3$
Pour $t$ variant de $- 1$ à $1$ , x(t) = 1.
pour $t$ variant de $1$ à $3$ , x(t)= 0.

Remarque : Pour vérifier la moyenne d'un signal carré, il suffit de tracer l'horizontale qui partage les zones en deux aires égales. On obtient ici $12\dfrac{1}{2}$ .

@Noemi ahh d'accord merci beaucoup