Sinus ou pas sinus, telle est la question
-
Philémon Robillard dernière édition par Philémon Robillard
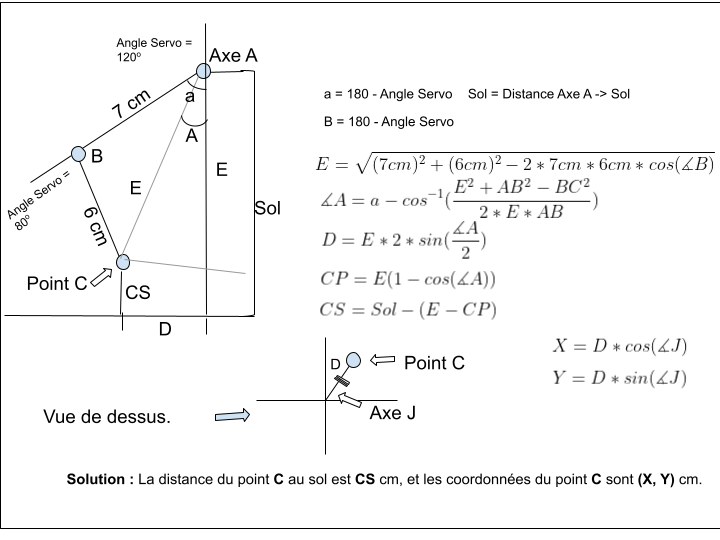
Bonjour, Je m'appelle Philemon et je suis en train de travailler sur un projet de robotique. Mon projet consiste à déterminer les équations des angles a et B du modèle montré dans l'image. Les informations connues sont D, CS, Sol ainsi que les coordonner (X, Y) du point C (Montré dans l'image).
Merci pour toute aide éventuelle !
-
BBlack-Jack dernière édition par
Bonjour,
Ce n'est pas clair.
La lettre E est utilisée 2 fois sur le dessin ??
Le point P n'est pas défini
...
-
Philémon Robillard dernière édition par
@Black-Jack Bonjour ! Comme vous l’avez remarqué, E est bel et bien utilisé 2 fois. Pour ce qui est de la lettre P, elle n’en a pas de telle lettre. Les longueurs dans le dessin sont : AB, BC, CP, CS, E, D, Sol, et les angles sont A, C, et a. J’espère que cela clarifie davantage le problème !
-
@Philémon-Robillard Bonjour,
Une piste :
A partir des relations indiqués,
déduire en premier E−CP=CS−SolE-CP= CS-SolE−CP=CS−Sol ce qui permet d'écrire l'expression de EcosAEcosAEcosA
On utilise ensuite la relation trigonométrique : 2sin2(A2)=1−cosA2 sin^2(\dfrac{A}{2})=1-cosA2sin2(2A)=1−cosA qui nous permet d'écrire une relation d'inconnue EEE.
La relation EEE trouvée, on peut déduire l'angle AAA puis l'angle aaa et l'angle BBB.