variation d'une fonction

Bonjour,
f(x)=2x/(3x+1)
Sans étudier les variations de f, je dirai qu'elle est décroissante car 3x+1>2x.
Finalement je me trompe!
Dans un QCM, j'aurai eu zéro !
Merci d'avance.

@kadforu a dit dans variation d'une fonction :

je dirai qu'elle est décroissante car 3x+1>2x.

Bonjour,

Pourquoi dis-tu que "je dirai qu'elle est décroissante car 3x+1>2x"

D'abord c'est faux
3x+1 > 2x si x > -1
et
3x+1<2x si x < -1

Il faut commencer par voir que Df = R/{-1/3}
et couper l'étude en deux.
Etudier pour x < -1/3
et
Etudier pour x > -1/3

...

Bonjour,
Je sais faire ce que tu as mentionné (je sais bien faire l'étude d'une fonction).
Tout simplement, je voulais dire: " il ne faut pas jugé d'un seul coup d'oeil."

@kadforu a dit dans variation d'une fonction :

Bonjour,
Je sais faire ce que tu as mentionné (je sais bien faire l'étude d'une fonction).
Tout simplement, je voulais dire: " il ne faut pas jugé d'un seul coup d'oeil."

Il ne faut, en effet, pas se précipiter pour répondre ...
Ici tu vois ce qui peut alors arriver.
Mais l'intérêt ici est quand même là, cela te devrait te permettre de réfléchir à l'erreur de raisonnement que tu as faite ... pour ne plus la refaire ultérieurement.

Surtout dans ce genre d'exo hésite pas à le refaire un peu plus tard pour voir

Bonjour tout le monde,

@kadforu, effectivement, une réponse précipitée est à éviter..
Sans faire l'étude mathématique, tu pourrais donner un "coup d'oeil" sur ta calculette graphique.
Elle te donnerait une réponse exacte.
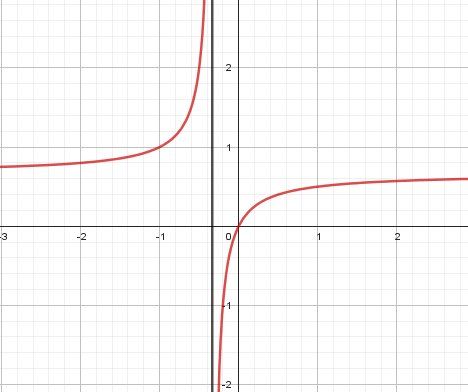
La représentation graphique de f est en rouge.
La droite en noire d'équation $x=−13x=\dfrac{-1}{3}$ est l'asymptote "verticale" correspondannt à la "valeur interdite"

Merci pour vos commentaires !

@kadforu , une remarque non demandée :

Si tu voulais étudier f sans utiliser la dérivée et son signe, c'est possible en transformant f(x) et en connaissant les fonctions usuelles.
$f(x)=2x3x+1=23(xx+1/3)\displaystyle f(x)=\dfrac{2x}{3x+1}=\dfrac{2}{3}\bigg(\dfrac{x}{x+1/3}\bigg)$

$f(x)=23(x+1/3−1/3x+1/3)\displaystyle f(x)=\dfrac{2}{3}\bigg( \dfrac {x+1/3-1/3}{ x+1/3} \bigg)$

Après transformation :
$f(x)=23(1−13x+1)\displaystyle f(x)=\dfrac{2}{3}\bigg(1-\dfrac{1}{3x+1}\bigg)$

Sur $]−∞,−1/3[]-\infty,-1/3[$ et sur $]−1/3,+∞[]-1/3,+\infty[$ :

x -> $3 x + 1$ est croissante
donc :
x -> $13x+1\dfrac{1}{3x+1}$ est décroissante

x -> - $13x+1\dfrac{1}{3x+1}$ est croissante

x -> 1 - $13x+1\dfrac{1}{3x+1}$ est croissante

x -> $23(1−13x+1)\dfrac{2}{3}\bigg(1-\dfrac{1}{3x+1}\bigg)$ est croissante

Conclusion : f est croissante sur chacun des deux intervalles considérés.

*Bonne réflexion @kadforu , si ça t'intéresse...

C'est une autre méthode que je ne connaissais pas mais elle est plus longue !

@kadforu

Tout à fait !
C'est une façon sans la dérivée, pour le plaisir de faire autrement, mais c'est plus long.

Mais on peut l'utiliser juste pour quelques fonctions ?

@kadforu
Pour les fonctions qui peuvent se décomposer facilement avec des fonction usuelles (connues).
Cela n'a rien de général, contrairement à la méthode avec la dérivée et son signe;