Résoudre un problème d'optimisation à l'aide des fonctions

Bonjour à tous,

Je tiens à dire que je suis nouveau sur ce forum.

Voici l'exercice qui me pose problème :

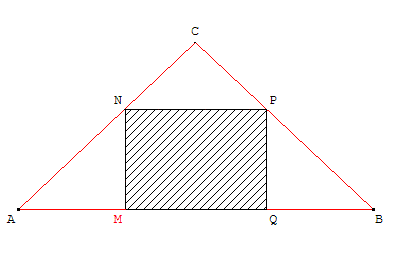
voici l'énoncé :

"ABC est un triangle rectangle et isocèle en C tel que AB = 10.
Soit J est le milieu de [AB] et M est un point de [AJ]. On note x la longueur AM.
On construit le rectangle MNPQ inscrit à l'intérieur du triangle ABC : N sur [AC] ; P sur [BC] et Q sur [JB].
Quelle est la position du point M sur [AB] pour laquelle l'aire du rectangle MNPQ est maximale ?"

Voila voila pour les citations, je pense qu'il faut que le point M soit placé tel que AM=MN ou bien MN=x. M'enfin ce ne sont que des suppositions.
Je bloque sincerement sur cet exercice.

Merci de votre prochaine aide.

@+

[amélioration de l'image, NdZ]

Bonjour,

A partir de AM = x, calcule la mesure de MN. Puis exprime l'aire du rectangle MNPQ en fonction de x.

Noemi
Bonjour,

A partir de AM = x, calcule la mesure de MN. Puis exprime l'aire du rectangle MNPQ en fonction de x.

Comment peux-tu calculer MN a partir de AM=x ??

J'ai noté à partir de AM = x, pour indiquer qu'il faut utiliser une relation utilisant AM
(Trigonométrie, Thalès, .....)

Noemi
J'ai noté à partir de AM = x, pour indiquer qu'il faut utiliser une relation utilisant AM
(Trigonométrie, Thalès, .....)

OK, j'ai trouvé ceci : ((xJC)/5)(10-2x) = A(mnpq), c'est bien cela ?

A quoi correspond JC ?

Noemi
A quoi correspond JC ?

Et bien, en utilisant Tahles, je parviens a exprimer MN en fonction de x et JC :

AJ/AM = JC/MN d'ou MN = (x*JC)/AJ (AJ=5)

De plus MQ=10-2x

Voila

JC c'est la hauteur ?

Quelle est la mesure de JC ?

JC est même la médiane, c'est donc une constante pour notre fonction finale. On peut donc faire le calcul sans prendre la valeur de JC en compte, celle-ci n'étant pas donnée .

Tu peux donner la valeur de JC, le triangle ABC est rectangle isocèle.

Noemi
Tu peux donner la valeur de JC, le triangle ABC est rectangle isocèle.

d'accord, je pense avoir compris et résolu l'exercice : JC est donc égal a 5, ce qui nous donne comme fonction finale : f(x) = 10x-2x² je trouve la dérivée de cette fonction : f'(x) = 10-4x = 2(5-2x). ici 2 est une constante, sa dérivée est donc nul.

On trouve finalement xmax = 5/2. après avoir posé le tableau de variation de la fonction.

C'est le résultat.

Noemi
C'est le résultat.

d'accord, c'est deja une bonne nouvelle, donc que dois-je dire pour répondre précisément à la question de l'exercice : Quelle est la position du point M sur [AB] pour laquelle l'aire du rectangle MNPQ est maximale ?"

Tu as trouvé la valeur de x, donc tu peux déduire la position du point M.

Noemi
Tu as trouvé la valeur de x, donc tu peux déduire la position du point M.

c'est curieux car on dirait pas sur la figure que le point M se situe a 2,5 du point A ... bizarre :rolling_eyes:

La figure ne donne pas le résultat mais juste une possibilité.

d'accord d'accord, et bien merci beaucoup pour ton aide et bonne fin d'après midi a toi.

bye