Geometrie - symetrie

Bonjour,
j'ai un DM de géometrie à rendre pour le 06/11. J'ai déja beaucoup cherché mais je n'arrive pas à le résoudre avec les seules données de l'enoncé. Je n'y arrive pas sans poser des hypotheses supplémentaires :
que O est centre de ABCD
que P est centre de ABEF, Q centre de ADHG, R centre de CDIJ et S centre de BCKL

Mais je ne sais pas si c'est autorisé

Voici tout le début de l'énoncé :

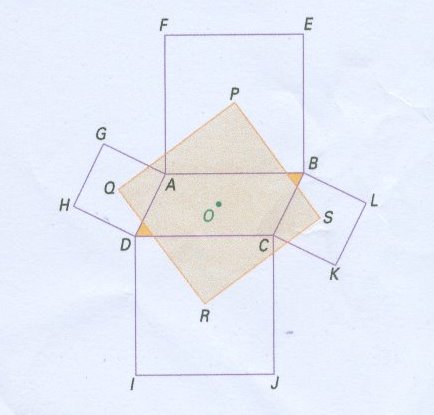
Le but de cet exercice est de démontrer que le quadrilatère PQRS est un carré, la figure étant constitué de quatre carrés construits exterieurement au parallalogramme ABCD.

on considere la symetrie de centre O
a) quelles sont les images des points A et B ? ->
facile si O est centre de ABCD
b) justifier que l'image du point E est le point I ->
facile si O est centre de ABCD
c) en déduire que l'image du point P est le point R ->
facile si P et R sont centre de ABEF et CDJI

Merci pour votre aide

$fichier math$

Bonjour,

Si tu ne connais pas la position du point O, tu ne peux pas trouver les images des points par une symétrie de centre O.
Sauf graphiquement.

merci
mais généralement les profs ne veulent pas que l'on se serve de graphique si ce n'est pas precisé.
Si on pose uniquement que O est centre de ABCD peut-on s'en sortir sans poser comme hypothese que P et R sont centre de ABEF et CDJI ?

Non,

Tu dois aussi faire ces hypothèses.
L'énoncé écris de ton exercice est complet ?

Oui et c'est bien ça mon problème

Si je pose toutes ces hypotheses c'est facile, mais on m'a toujours interdit de faire ça.

C'est dans le livre Maths reperes $2^{de}$ exo 65 page 81

Dois-je mettre un scan complet de l'exercice ?

Non

le scan de l'énoncé n'est pas autorisé.
Vérifie que tu as bien donné tout l'énoncé.

j'ai bien vérifié : il manque seulement la suite des questions

dois-je l'écrire ?

Oui
Indique les autres questions.

Voici toute la suite

d) Que peut-on deduire de la nature du quadrilatère PQRS

On note α le mesure de l'angle BPS
a) Montrer que les triangles PBS et PAQ ont en commun les longueurs de deuc cotés adjacents à un angle de même mesure.
On admet alors que ces deux triangles sont superposables.
b) Que peut on alors en déduire à propos de la mesure des angles BPS et APQ, et de la longueur des cotés PQ et PS.
c) En déduire que le quadrilatère PQRS est un losange
d) Montrer que QPS = 90°
e) conclure sur la nature du quadrilatère PQRS

J'ai déja un peu cherché à partir du 2) mais j'ai du mal à comprendre la question 2)a)

Question 2 a) analyse les deux triangles, leurs côtés et angles .

si on suppose que P centre de ABEF donc PB et AP ont même longueur.
si on suppose que S centre de BCKL, et que Q centre de ADHG donc BS et AQ ont même longueur.
mais comment fait on pour les angles ?

Pour l'angle PBS, tu le décomposes en trois angles.
L'angle PBA = ....

PBA = PAF = QAG = SBC = 45 °

mais comment continuer ? angles CBA? et GAF ?

Analyse les angles autour du point A.

OK merci

Donc si on regarde le triangle DAB
et que l'on fait la somme des angles autour du point A

on peut en deduire que GAF = ADB+ABD = ABC

Oui l'angle GAF = l'angle ABC.

Merci pour tout, je devrai m'en sortir maintenant

c'est très gentil d'avoir pris tu temps pour moi