Points sur un cercle

Bonjour a tous,
Pouvez-vous m’aider à résoudre ce probléme ?
Soit 4 points A,B,C,D situé sur un cercle, tel que les droites AB et CD ne sont pas parallèles.
On trace la droite passant par D et parallèle à AB : elle recoupe le cercle en E
on trace la droite passant par E et parrallèle à BC : elle recoupe le cercle en F
On trace la droite passant par F et parallèle à CD : elle recoupe le cercle en G
démontré que G et A sont confondus.
Merci à ceux qui m’aiderons.

Bonsoir,

As-tu fais une figure ?
Compare les mesures des angles.

Bonjour,

C'est vraiment un exercice de Terminale S ? Cela me semble étrange ! PEux tu nous préciser dans quel forum il faut déplacer ce sujet ! Merci.

C'est pour un ami en suisse
J'essai de poster la figure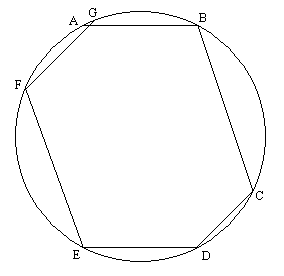

points sur un cercle
angle B = angle E
angle C = angle F

Personne ?

Up !

Bonsoir,

Voila une solution bien detaille pour cet exercice

angle(EBA) = ( arc(AF) + arc(FE) ) / 2 (angle inscrit qui intercepte l'arc AE)

or angle(EBA) = angle(BED) ( angles internes internes )

comme angle(BED) = ( arc(BC) + arc(CD) ) / 2 (angle inscrit qui intercepte l'arc BD)

et comme arc(CD) = arc(EF) (car deux droites paralleles determinent entre elles deux arcs de meme mesures)

par suite arc(AF) = arc(CD) et comme arc(CD) = arc(FG) alors arc(AF) = arc(FG)

d'ou A et G sont deux points confondus

Bonne chance

Citation
et comme arc(CD) = arc(EF)
Ben non ces deux arcs ne sont pas égaux, sa se voit sur le dessin

Bonsoir,

Oui tu as raison

"et comme arc(EF) = arc(BC) (car deux droites paralleles determinent entre elles deux arcs de meme mesures)"

et la meme demonstration reste vraie

A bientot

Non plus : arc (EF) n'est pas égal à arc(BC) : il faudrait que les deux cordes EF et BC est la même longueur : il n'a pas de raison.
De plus, il y a deux arcs de même nom ( deux arc EF , deux arcs Bc , )
et les égalités dépende de la position des points.

Bonsoir,

Je veux ecrire les arcs toujours dans le sens positifs

(BC) parallele a (EF) donc arc(BF) = arc(EC)
donc arc(BA) + arc(AF) = arc(ED) + arc(DC)

(AB) parallele a (ED) donc arc(AE) = arc(DB)
donc arc(AF) + arc(FE) = arc(DC) + arc(CB)

(CD) parallele a (FG) donc arc(FD) = arc(CG)
donc arc(FE) + arc(ED) = arc(CB) + arc(BG)

Par suite on a le systeme forme de trois equations suivants

arc(BA) + arc(AF) = arc(ED) + arc(DC) (1)
arc(AF) + arc(FE) = arc(DC) + arc(CB) (2)
arc(FE) + arc(ED) = arc(CB) + arc(BG) (3)

En faisant (1) - (2) on aura arc(BA) - arc(FE)= arc(ED) - arc(CB) (4)
arc(FE) + arc(ED) = arc(CB) + arc(BG) (3)

en faisant (3) + (4) on aura arc(BA) + arc(ED) = arc(ED) + arc(BG)
Par suite arc(BA) = arc(BG)

d'ou A et G sont deux points confondus ce qu'il faut demontrer

A bientot

Cette fois ça me paraît juste, à condition comme tu le dit de supposé tout les arcs dans le même sens.
Alors c'est comme les angles à 2k $p i$ près ?
En tour cas merci.