Démontrer que deux droites sont orthogonales
-
Iindetectable dernière édition par Hind
Bonjour, voilà dans ma classe de 1ère S depuis 1 semaine on a commencé la géométrie dans l'espace mais je suis complétement pedu je déteste la géométrie.
J'ai un exercice pour lundi que j'ai fais mais je sais pas si j'ai bon si vous pouvez m'aider sa serait gentil
Enoncé :
Démontrer que (EG) est orthogonale à (BFH)
En déduire que (DF) est orthogonale à (EG)Mes réponses sont :
(EG)⊥(HF)
(EG)⊥(BF)
(HF) et (BF) sont sécantes dans (HBF)
Donc (EG)⊥ (HBF)(DF)⊥(EG)
(AC)⊥(EG)
donc (AC)⊥(DF)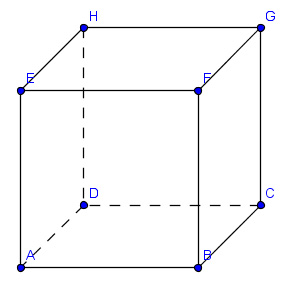
-
Mmathtous dernière édition par
Bonjour,
tu peux regarder ici :[Orthogonalité de droites et de plans](http://dmat.perso.neuf.fr/articles/Orthogonalite de droites et de plans.pdf "Orthogonalité de droites et de plans")
-
Iindetectable dernière édition par
Je comprend pas mon erreur oO
-
Mmathtous dernière édition par
Citation
En déduire que (DF) est orthogonale à (EG)Et toi tu pars de ce qu'il faut démontrer ! :
Citation
(DF)⊥(EG)Il y a d'autres erreurs ou imprécisions.
-
Iindetectable dernière édition par
Démontrer que (EG) est orthogonale à (BFH) c'est bon sa ?
Je cherche pour En déduire que (DF) est orthogonale à (EG)

-
Mmathtous dernière édition par
Pour la première question : oui et non.
Tu dois
justifiertes réponses.Pourquoi (EG) est-elle orthogonale à (HF) ?
-
Iindetectable dernière édition par
(EG) orthogonal à (HF) car (AC) parallèle à (EG) et (DB) parallèle à (HF) et (AC) et (DB) sont perpendiculaire c'est bon cela ?

En déduire que (DF) est orthogonale à (EG)
(DF)⊥(EG)
car (AC) parallèle à (EG)
et (AC) ⊥(DF)
-
Mmathtous dernière édition par
Citation
(EG) orthogonal à (HF) car (AC) parallèle à (EG) et (DB) parallèle à (HF) et (AC) et (DB) sont perpendiculaire c'est bon cela ? :DNon : tu ne fais que déplacer le problème, toujours sans justifier les intermédiaires.
(EG) ⊥(HF) c'est la même chose que de démontrer que (AC)⊥(DB).Je suppose que la figure représentée est un cube ?
Que sont les faces d'un cube ?
-
Iindetectable dernière édition par
Oui c'est un cube j'ai attaché une figure à l'énoncé.
Les faces sont des carrés
-
Mmathtous dernière édition par
Quelles sont les qualités ( les propriétés ) d'un carré ?
Du moins celles qui vont te servir à démontrer que (EG)⊥(HF) ?
-
Iindetectable dernière édition par
Les diagonales d'un carré forment un angle droit
-
Mmathtous dernière édition par
Oui.
Ensuite, tu dois justifier que (EG)⊥(BF).
Que peux-tu dire de la droite (BF), sachant que ABCDEFGH est un cube ?
Plein de choses , mais choisis.
-
Iindetectable dernière édition par
(FB) perp à la face EFGH
donc (FB) ortho à toutes droites du plan (EGF)
donc (FB) ortho à la droite (EG) au plan (EGF).
-
Iindetectable dernière édition par
En déduire que (DF) est orthogonale à (EG)
(DF)⊥(EG)
car (AC) parallèle à (EG)
et (AC) ⊥(DF)Cela est-il juste ?
-
Mmathtous dernière édition par
OK
La suite convient : (EG) est orthogonale à deux droites sécantes du plan HBF ( les droites (HF) et (BF) ) , donc elle est orthogonale à ce plan.Pour la question suivante
Citation
En déduire que (DF) est orthogonale à (EG)je t'ai dit plus haut que ton raisonnement ne convient pas puisque tu commences par ce qu'il faut démontrer.Que viens-tu de démontrer sur la droite (EG) ?
Qu'en résulte-t-il ?
-
Iindetectable dernière édition par
La droite (EG) est orthogonale à toute les droite du plan (BFH) donc (EG) ⊥(DF)
-
Mmathtous dernière édition par
Oui.
-
Iindetectable dernière édition par
Merci de ta patience

-
Mmathtous dernière édition par
De rien.
A+