Géométrie, fonction...
-
MMarineC dernière édition par
On considère un carré ABCD de côté 1.
Soit M un point variable du segment [AB].
Le réel x représente la longueur AM.
Soit H le projeté orthogonal de M sur [DC].
Soit O le point d'intersection de (HM) et (AC).
Soit N le projeté orthogonal de O sur [AD].
Soit P le point d'intersection de (NO) et (BC).
On considère les fonction de x: f, g, h, et k ainsi définie :
f(x) est l'aire de l'hexagone ABPOHD.
g(x) est l'aire du quadrilatère AMON.
h(x) est l'aire du triangle OHC.
k(x) est l'aire du quadrilatère ADHB.II-) Réaliser une figure et l'utiliser pour calculer f(x) en fonction de x.
III-)Réaliser une figure et l'utiliser pour calculer g(x) en fonction de x.
**IV-)**Réaliser une figure et l'utiliser pour calculer h(x) en fonction de x.
v-) Réaliser une figure et l'utiliser pour calculer k(x) en fonction de x.
(VI- Dans un même repère orthonormal, en prenant 10cm pour unités sur les deux axes, tracer, dans quatre couleurs différentes et légendées, les courbes représentatives de f, g, h et k.) *ça j'ai vraiment pas compris comment on fait mais il faut les réponses aux questions d'avant pour y arriver je pense..
*
Merci a celui ou celle qui pourra m'aider la dessus..
-
Zorro dernière édition par

Bonjour, cela se dit !
si tu as bien fait ton schéma cela devrait ressembler à :
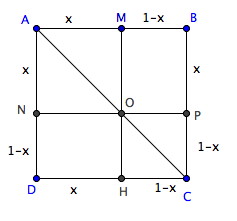
A toi de démontrer que les mesures sont bien x et 1 - x
Avec ces dimensions , calculer les aires demandées par somme ou différence d'autres aires devrait être plus facile.
-
MMarineC dernière édition par
Oki donc est-ce que ca donne ca:
f(x) : (AB x BP) + (NO x ND) =(1X) + (X1-X )
g(x): (AM x AN) = (X * X) = X²
h(x): (OH x OP)/2 = (1-X * 1-X)/2 = (1-X)²/2
k(x): (AB x AD) - (HC x CB)/2 = (1x1) - (1-X* 1)/2 =1-(1-X*1)/2
-
Zorro dernière édition par

Pense à mettre des ( ) au bon endroit dans (1X) + (X1-X ) ... car ce n'est pas vraiment la bonne réponse !
-
MMarineC dernière édition par
???
-
Bonjour,
Applique la consigne indiquée par Zorro, soit "mettre des parenthèses au bon endroit" puis simplifie les expressions.
-
MMarineC dernière édition par
Oui mais elles sont pas au bon endroit la ??
-
Les mesures des côtés sont 1, x et 1-x, chaque fois que tu utilises 1-x note (1-x).
-
MMarineC dernière édition par
Donc:
f(x) : (AB x BP) + (NO x ND) = (1X) + [ X(1-X) ]
g(x): (AM x AN) = (X * X) =X²
h(x): (OH x OP)/2 = (1-X * 1-X)/2 = (1-X)²/2
k(x): (AB x AD) - (HC x CB)/2 = (1x1) - (1-X* 1)/2 = *1-[(1-X)1]/2
-
Tu peux simplifier l'expression de f et k.
-
MMarineC dernière édition par
f(x) : X * (X-X²) =X² - X³
k(x): 1-(1-X) /2
-
f est faux ce n'est pas une multiplication
k réduis au même dénominateur.
-
MMarineC dernière édition par
f(x) : (1X) + [ X(1-X) ] = X + (X-X²)
k(x):1-(1-X)/2 = au même dénominateur : 1x2/2 - (1-X)/2
= 2-1+X/2
= 1+X/2
-
f(x) = x +x - x² = ...... on peut simplifier
k(x) = (1+x)/2
-
MMarineC dernière édition par
Roooh

Alors:
f(x) = 2x-x²
k(x)= (1+x)/2
-
Oui c'est le résultat.
-
MMarineC dernière édition par

donc c'est bon je les ai tous !
Maintenant j'ai juste une question pas pour les résultats mais juste que je comprends pas trop ce que ca veut dire.Dans un même repère orthonormal, en prenant 10cm pour unités sur les deux axes [...}
Quand il dise "en prenant 10cm pour unité" ca veut dire quoi ?
-
MMarineC dernière édition par
Est-ce que ca veut dire que je dois prendre 10cm pour les chaque axes et les diviser en fonction des résultats obtenu ?
-
Sur les deux axes, une unité correspond à 10 cm.
-
MMarineC dernière édition par
Mais c'est quoi une unité ?
-
Une unité c'est 1
Le côté du carré mesure 1, donc x varie de 0 à 1.
-
MMarineC dernière édition par
Après ils nous dise de regarder grace a un tableau de variation pour quel valeur de x f=h; f=k et pour g=h et de faire un encadrement a 0,01 près.
Je l'ai fais et j'ai trouver :
pour f=h : 0,17< x <0,18
pour f=k : 0,49< x <0,51
pour g=h: 0,41< x <0,42Mais la question d'après c'est "[b]Interpréter géométriquement les résultats de la question précédente[/b]."
Mais j'ai pas compris mais alors pas du tout qu'est-ce qu'ils veulent que je fasse..
-
Quand tu as l'égalité des fonctions, que peux tu dire sur les aires des polygones ?