Les Barycentres

Bonjour ! J'ai un DM a faire pour dans quelques jours sur les barycentres et je n'arrive pas à résoudre certaines questions. Par exemple pour la question 1 je sera le faire s'il y avait des données sur des points, mais là je ne comprend pas, merci de m'expliquer.

ABC est un triangle. I est le milieu de [BC], G est le centre de gravité de ABC.

Déterminer l'ensemble E des points M du plan tels que :
||MB $→^\rightarrow$ + MC $→^\rightarrow$ || = ||3 MB $→^\rightarrow$ - MC $→^\rightarrow$ ||

2)a) Montrer que V $→^\rightarrow$ = 2MA $→^\rightarrow$ - MB $→^\rightarrow$ - MC $→^\rightarrow$ ne dépend pas du point M en exprimant V $→^\rightarrow$ en fonction de IA $→^\rightarrow$

b) Déterminer l'ensemble F des points M du plan tels que :
||MA $→^\rightarrow$ + MB $→^\rightarrow$ + MC $→^\rightarrow$ || = || 2MA $→^\rightarrow$ - MB $→^\rightarrow$ - MC $→^\rightarrow$ ||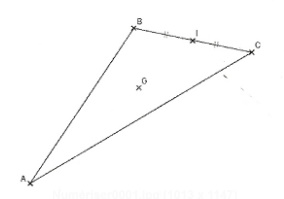

$fichier math$

Bonjour,

Modifie tes relations vectorielles en utilisant le barycentre de points.

salut

1°

en gras, des vecteurs...

MB + MC = 2 MI

peut-être introduire un barycentre dans 3 MB - MC...

2°

a) relation de Chasles avec le point I dans expression de V.

b) MA + MB + MC = 3 MG

[rha doublon ; je laisse la main. NdZ]

Comment trouve t'on MB + MC = 2 MI ?

Tu appliques la relation de Chasles et tu prends en compte le fait que I milieu de [BC].

Merciiii !!!!

Pouvez vous me détailler les étapes pour arriver à MB + MC = 2 MI
Svp !

MB+MC = MI + IB + MI + IC
= .....

MB+MC = MI + IB + MI + IC
MB+MC = 2MI ( car IB+IC = vecteur nul)

Faut il faire pareil pour 3 MB - MC ?

Pour 3MB - MC, tu introduis un barycentre.

3MB - MC = 2 MG ???

Oui avec G barycentre des points .....

Alors la je sais pas comment on peut trouver ! :s

Tu as écrit : 3MB - MC = 2 MG,
donc G est le barycentre de (B;3) et (C;-1)
Soit 2||MI|| = 2|| MG||
Ou MI = MG
Donc M ......

Pour moi,

MI = MG
donc E est la médiatrice du segment [IG]

POur la question 2) b)
Est ce que MA + MB + MC = 3 MG
et 2MA - MB - MC = 2IA ???

Oui c'est correct.

Pour la dernière question on a donc

F= {MA + MB + MC = 2MA - MB - MC }
F = {3 MG = 2IA }

Quelle peut etre la conclusion ?

MG = 2IA/3
IA est constant,
donc ....

donc MG = 2/3 ?

Non

Un point M (lié à un point G) qui se déplace ....

Je ne comprend pas :s

MG = 2/3 IA, équation d'un cercle de centre .... et de rayon .....

MG = 2/3 IA, équation d'un cercle de centre I et de rayon 2/3 cm ??

Non :
MG = 2/3 IA, équation d'un cercle de centre G et de rayon 2/3 IA.

Merci beaucoup pour votre aide !