Démontrer que des droites sont perpendiculaires

Bonjour,
Je n'arrive pas à resoudre un exercice de géométrie , il faut dans un premier temps construire la figure , je vous marque l'enoncé pour que vous visualisez la figure :

"Soit ABC un triangle non aplati, I le milieu de [BC], H son orthocentre, G son centre de gravité et O le centre du cercle circonscrit. A' est le symétrique de A par rapport à O".

La figure je l'ai faite pas de problème mais par la suite on me demande de démontrer que les droites (AB) et (BA') sont perpendiculaires et que les droites (AC) et (CA') sont perpendiculaires ,je n'y arrive pas !
Merci d'avance pour vos explications .

Bonjour,

Analyse les côtés du triangle ABA'.

Bonjour ,
[AA'] est un diamètre étant donné qu'il passe par O , mais je ne vois pas ou vous voulé en venir ?

Que peut-on dire de BO ?

Que c'est un rayon du cercle circonscrit

Et par rapport au triangle ?

c'est la moitié du segment [AA']

Que peut-on en conclure sur la nature du triangle ABA' ?

Que le triangle est rectangle en A' .
c'est ce qui va me permettre par conséquent de dire que les deux droites sont perpendiculaire non ?

Précise la propriété que tu utilises, puis conclue que les droites sont perpendiculaires.

Merci beaucoup pour votre aide , par contre dans une autre question du même exercice on me demande cela : " Rappeler la position du centre de gravité d'un triangle sur chacune de ses médianes " , pourriez-vous m'expliquer cette question , je ne la comprend pas .
Merci
Bonne soirée

Quelle est la position du centre de gravité par rapport à la médiane ?
Quelle relation y a t'il entre les mesures de AI et AG ?

Merci , par contre serait-il possible que vous m'aidiez à finir mon exercice , sans me donner les réponses loin de là , mais juste en me l'expliquant ; car je suis vraiment perdu dans cet exercice qui doit , à la fin , démontrer que le centre de gravité , l'orthocentre et le centre du cercle circonscrit sont alignés sur une même ligne : la droite d'Euler .
Merci d'avance.

Bonjour,

Indique tes éléments de réponse et on te donnera des conseils pour la résolution.

Bonjour ,

Merci beaucoup c'est gentil !
On me demande de démontrer que les droites (BH) et (CA') sont parallèles , mais je ne vois pas grâce à quoi je peux répondre .

Salut

Avec une figure ça ira mieux

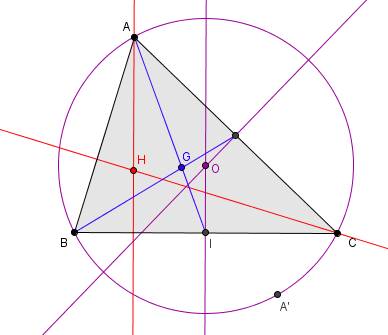
(BH) et (CA') sont parallèles: à toi de compléter !

(BH) est une ... dans ABC, donc il y a un angle droit entre (BH) et (...)

(AA') est un ... du cercle, donc il y a un angle droit entre (CA') et (...)

donc (BH) et (CA') sont toutes deux ... à la même droite (...) : elles sont donc PARALLELES (j'avais initialement écrit : perpendiculaires lol).

Merci beaucoup pour votre aide , je le farai plus tard car je pars féter Noel , Bonne fête à vous & merci encore !

Bonjour,

Je suis arriver à compléter les deux première phrases , merci beaucoup , mais j'ai un petit problème avec la dernière que je n'arrive pas à résoudre .

Bonjour,

Peux-tu indiquer la question qui te pose problème ?

Oui biensur excuser moi c'est celle où Zauctore m'a aider en me donnant le texte à trou que j'ai compléter part contre j'ai un petit soucis car je n'arrive pas à compléter cette phrase "donc (BH) et (CA') sont toutes deux ... à la même droite (...) : elles sont donc perpendiculaires. "
Merci .

Une erreur dans la conclusion, il faut lire elles sont donc parallèles (à la place de perpendiculaires).

ah oui vous avez raison , merci . Mais je n'arrive pas à compléter : " (BH) et (CA') sont toutes deux ... à une même droite (...) "
Je ne vois pas quel rapport peut -il avoir entre ces deux droites .

Tu as des angles droits donc les droites sont .......
par rapport à quelle droite .... ?

ah oui merci , je n'avais pas vu qu'elles étaient perpendiculaire à (AC) .
Ensuite on me demande de démontrer que les droites (BA') et (HC) sont parallèle . J'avais commencer à faire comme la question précédente , mais je me suis rendu compte que ce n'était pas cela . Merci beaucoup .

C'est le même type de démonstration. Indique tes calculs.

Je ne comprend pas quel calcul vous me demandez de faire?
Désolé

re.

(BA') et (HC) sont toutes les deux perpendiculaires à (AB)

donc...

Merci beaucoup j'ai enfin trouvé.
On me demande par la suite de démontrer que I est le milieu de AH,je ne vois pas quel argument je pourrai donner pour démontrer cela.
Merci et bonne soirée

Vérifie l'énoncé "I milieu de AH" ??

bonjour,
dans mon enoncé ,c'est I milieu de [HA']"
merci

Quelle est la nature du quadrilatère BHCA' ?

C'est un parallélogramme et I est le point ou se coupe les deux diagonales du quadrillatere ,mais je ne vois pas comment justifier cela .
merci

Par hypothèse, I est le milieu de [BC] donc ....

Justifier que BHCA' est un parallélogramme, marjorie ?
on doit pouvoir prouver que les côtés opposés sont deux à deux parallèles, non ?

bonsoir,étant donné que les 2 diagonales d'un parallélogramme se coupent en leur milieu qui est donc I ,j'en conclu que I est le milieu de [BC] mais aussi celui de [HA'].Cette justification est elle bonne?
MERCI

I est le milieu de [BC] est une donnée de l'énoncé.

Mais je ne vois vraiment pas qu'elle propriété du parallélogramme je dois utiliser , Car je pensais que la justification que je vous ais envoyer été la bonne . :frowning2:
Merci

La propriété est la bonne, mais c'est que tu écris "j'en conclus que I est le milieu de BC" Or l'énoncé indique que I est le milieu de BC.
[HA'] et [BC] sont les diagonales du parallélogramme, I est le milieu de [BC] donc I est le milieu de [HA'].

Bonjour,
Ah oui merci je vois mieux mon erreur , merci beaucoup .
Dans le question suivante on me demande de Rappeler le position du centre de gravité d'un triangle sur chacune de ses médianes .
Ma réponse est " le centre de gravité se situe au 3/4 de la médiane , Par conséquent AG = 3/4 AI" .Je suis arrivé a répondre à cette question grâce à aux indications que vous m'avez fournis au début .
Mais par contre la question d'après me pose encore un problème car on me demande de démontrer que G est le centre de gravité du triangle AHA' , je ne sais pas sur quoi je dois me baser pour répondre à cette question.
Merci beaucoup pour votre aide .

" le centre de gravité se situe au 3/4 de la médiane " en partant de la base ? du sommet ?
de toute façon ça m'étonnerait !!!