Translations et homothéties 1ère S

[astrakan]

Bonjour,

Mes meilleurs voeux pour la nouvelle année.

Je bloque sur un exercice sur l'homothétie.

Soit une pavé ABCDEFGH tel que AB<bC et un point M de l'arête [AB], distinct de A et de B.
On construit le point I de la face ABCD et le point J de la face EFGH tels que les triangles AMI et [EFJ soient des triangles équilatéraux.
En utilisant une homothétie bien choisie, démonter que les droites (IJ),(AE) et (MF) sont concourantes.

Je joins l'image du pavé car je ne trouve la bonne homothétie pour démarrer l'exercice.

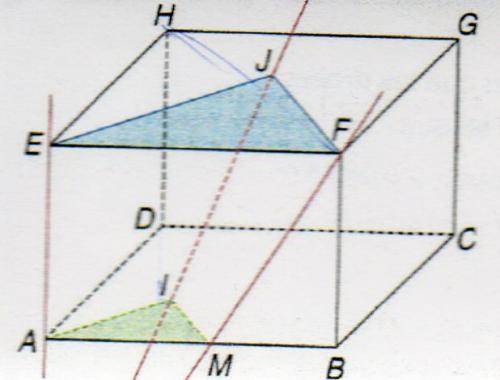
Merci de votre aide.

[Noemi]

Bonjour,

A partir du point d'intersection des droites (EA) et (FM), puis (JE) et (AI), écris les rapports des distances et montre que ce point est commun aux trois droites.

[astrakan]

Bonsoir,

Merci pour votre réponse.
Peux-t-on utiliser le choix du théorème sur les angles orientés ?
En considérant que les deux triangles ont leurs côtés parallèles deux à deux et comme ils sont équilatéraux vec(AM)=k vec(EF), vec(MI)=k vec(FJ), vec(IA)=k vec(JE).
On peut ainsi affirmer que le triangle AMI est l'image du triangle EFJ par l'homothétie de centre (le point d'intersection des droites) et de rapport k.
Les 3 droites sont ainsi concourantes.

[Noemi]

C'est correct.

[astrakan]

Merci et bonne soirée.