Barycentre / centre d'indertie
-
Ttibo42 dernière édition par
Bonjour
On considère une plaque homogène P qui est un disque de centre O et de rayon R. A partir de cette plaque P, on fabrique une nouvelle plaque P' en évidant la plaque P, comme l'indique la figure si dessous, d'un disque de rayon R/4 et de centre O'.
On appelle G le centre d'inertie de la plaque P'.**** Edit de Zorro : ce n'est pas ainsi qu'on envoie une image, ici *** ( image )
- a) Exprimer O comme barycentre de G et O'.
b) En déduire la position du point G.
On note m la masse de la plaque P'.
Quelle masse doit-on placer au point A pour que l'ensemble constitué par la plaque P' et le point A ait O pour centre d'inertie?Voila donc dès le début j'ai un problème de compréhension de l'énoncé.
Qu'est-ce que P' ? la plaque de rayon R/4 ou bien la plaque P moins la petite plaque de rayon R/4 ?Merci d'avance pour votre aide

-
Zorro dernière édition par

Bonjour,
Pour savoir comment envoyer un scan ou une image, ici, il faut lire le message écrit en rouge dans la page d'accueil ; clique sur ce qui est dessous c'est un lien
-
Ttibo42 dernière édition par
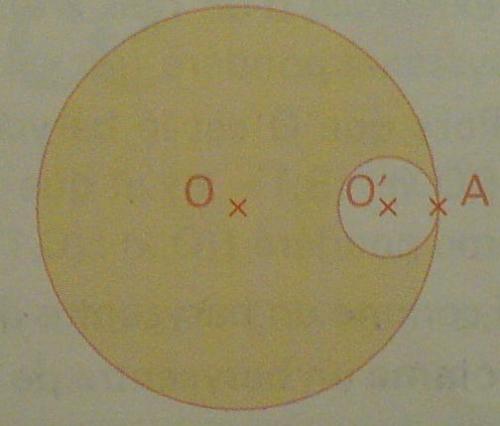
-
Zorro dernière édition par

Alors, que proposes tu ? Il faut trouver les réels a et b tels que
aOG→^\rightarrow→ + bOO'→^\rightarrow→ = 0→^\rightarrow→
-
Ttibo42 dernière édition par
Donc soit G1 le centre de gravité de P' et G2 le centre de gravité du cercle de rayon R/4
Soit m1 l'aire de P' et m2 l'aide du cercle de rayon R/4Alors G est le barycentre de (G1;m1)(G2;-m2)
Donc G barycentre de (G1; PiR²)(G2;-Pi(R/4)²)
Pi-R²G1G-(Pi*(R/4)²G2G)=0
ça a l'air vraiment bizarre... C'est juste ?
-
Ttibo42 dernière édition par
Re bonjour, j'ai réussi la question 1) a et b mais je bloque sur la 2) pour la masse de A
-
Ttibo42 dernière édition par
Re bonjour, j'ai réussi la question 1) a et b mais je bloque sur la 2) pour la masse de A
-
Bonjour,
Ecris la relation pour le centre d'inertie.
-
Ttibo42 dernière édition par
Je trouve 15OG + OO'= 0 (vecteur)
-
La relation doit prendre en compte le point A et le coefficient m.