Fonction, calcul d'aires

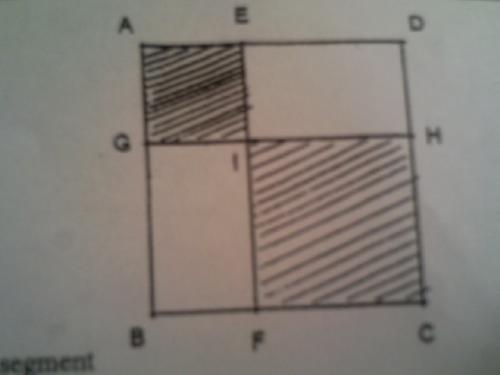
ABCD est un carré de côté 10 cm. E est un point du segment [AD] et G est un point du segment [AB] tel que AE =AG.
(EF) et (GH) sont respectivement parallèles à (AB) et (AD).
On appelle x la longeur AE en cm et S(x) l'aire totale de la surface hachurée sur le dessin ci-contre.

1°) Quelles valeurs prend la variable x ? On notera I cet intervalle.

2°) Montrer que pour tout x réel de I, on a : S(x) = 2 x² - 20x + 100

3°) Compléter le tableau de valeurs ci-dessous :

4°) a) Construire la courbe représentative de la fonction S dans un repère othogonal approprié.
b) Indiquer le tableau de variation de la fonction S. ( à partir du graphique)

5°)
a) Trouver graphiquement pour quelles valeurs de x l'aire S(x) vaut 52cm².* on laissera les traits de construction apparents.*
b) Montrer que pour x de I, on a : S(x) = 2 ( x - 5 )² + 50
c ) En utilisant cette expression, retrouver par le calcul les solutions de l'équations S(x) = 52

6°) Pour quelle valeur de x, l'aire totale de la surface hachurée est-elle minimale ? Conjecturer puis, en utilisant l'espression de S(x) trouvée précédemment à l'aide d'inégalités.

on se propose dans cette question de prouver la question 4b) par le calcul.

a) Soient u et v deux nombres de I tels que u < v ≤ S
Factoriser S(u) - S(v) par u - v puis donner le signe de chaque facteur et conclure sur le signe de S(u) - S(v).
En déduire alors le sens de variation de S.
b) Refaire le même travail avec u et v de I tels que 5 ≤ u < v

Bonsoir,

Indique tes éléments de réponse et la question qui te pose problème.

Bonjour,

Cela se dit encore au 21ème siècle !

A côté de ton pseudo, il y a un 1 qui clignote, cela veut dire que je t'ai envoyé en message privé. Si tu veux de l'aide , tu devrais le lire en cliquant dessus.

Bonnes lectures !