exercice fonction limite

je n'arrive pas les limites
pouvez vous m'aider s'ils vous plait

On considere la fonction f définie sur R par f(x)=1/3x4-2x²-2
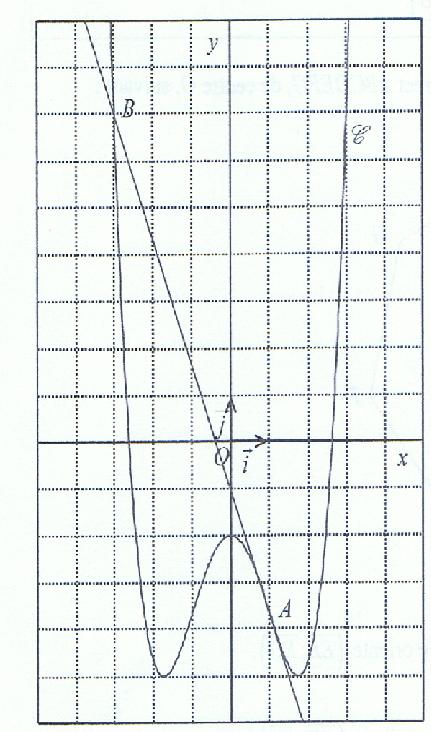
On donne ci dessous dans un repere(O,I,J) du plan une partie de la courbe représentative C de f et la droite (AB) passant par les points A et b de C d'abcisses respectives 1 et -3

1)démontrer que f est dérivable en 0 et indiquer le nombre dérivé f en 0

2)calculer le coefficient directeur de la droite (ab)
determiner lim h0 f(1+h)-f(1)/hj

que peut-on déduire pour f ?

c)en déduire que la droite (AB) est tangente en A à la courbe C

merci d'avance

j'ai juste fait ca pour le moment

f est définie sur R donc f est dérivable sur R
Donc f'(x) = 4/3x3- 4x
Donc f'(0) = 0

2)le coefficient est égale a

a=yb-ya/xb-xa

=7--4/-3-1=-11/4

voici la courbe pour aider

Bonjour,

Calcule :[ f(1+h)-f(1)]/h

j'ai trouvé 1/2

Indique ton calcul.

Vérifie le calcul pour le coefficient directeur de (AB) yA n'est pas égal à -4.

a oui ya=3

les limite ce n'est pas mon fort
je suis un peu perdu

f(1+h)-f(1)/h/h

f(1)+f(h)-f(1)/h

f(h)/h

Non
yA = -11/3

[f(1+h)-f(1)]/h n'est pas égal à [f(1)+f(h)-f(1)]/h
calcule f(1+h)-f(1)

f(1+h)-f(1)
f(1+0)-f(1)
f(1)-f(1)

Remplace dans l'expression de la fonction, x par 1+h et x par 1
Puis tu calcules
f(1+h) - f(1)

$1/3*(1+h)^4$ -2*(1+h)² $2-1/3<em>1^4$ -21²-2

Développe et simplifie l'expression.

$1/3(1+h)^4$ -2*(1+h)²-6-1/3

je suis un peu embrouillé la

Développe le terme à l'exposant 2 et celui à l'exposant 4.

$1/3+1+4h+h^4$ -2+1+2h+h²-6-1/3

$f(x)=1/3x^4$ -2x²-2
f(1+h) = $1/3(1+h)^4$ - 2(1+h)² - 2
= (1/3(1+4h+6h² $+ 4 h$ ^3 $h^4$ ) - 2(1+2h+h²) - 2
f(1) = -11/3

Calcule f(1+h) - f(1) = ....

pourqoui f(1+h)-f(h)

Une erreur de frappe :
C'est :
f(1+h) - f(1)

ca fait 1/3(1+4h+6h²+h3)-2(1+2h+h²)-17/3

f(1+h) = 1/3(1+h)4 - 2(1+h)² - 2
= (1/3(1+4h+6h² $+ 4 h$ ^3 $h^4$ ) - 2(1+2h+h²) - 2
f(1) = -11/3

f(1+h) - f(1) = 1/3(4h+6h² $+ 4 h$ ^3 $h^4$ ) - 2(2h+h²)

Tu calcules (f(1+h) - f(1))/h puis la limite quand h tend vers 0

je suis vraiment perdu la
je vais jamais arrivé

il faut factorisé?

quelqu'un pour m'aider s'ils vous plait
c'est a rendre pour demain

f(1+h) - f(1) = 1/3(4h+6h² $+ 4 h$ ^3 $h^4$ ) - 2(2h+h²)
et (f(1+h) - f(1))/h = 1/3(4+6h+4h² $h^3$ ) - 2(2+h)

Tu calcules la limite pour h qui tend vers 0

la limite pour h qui tend vers 0 est 1/3*4 -4
=4/3-4/4=4/12

Une erreur,
c'est 4/3 - 4
= -8/3

a oui merci

je ne vois pas ce qu'on déduit

il y a 1 calcul a faire?

Si tu compares le coefficient directeur de (AB) (Calcul à refaire car ton résultat est faux) est la limite, que remarques tu ?

le coefficient est égale a ya-yb/xa-xb

11/3-7/1--3

C'est :
(-11/3-7)/(1-(-3)) = ...
Fais le calcul

c'est égal a -(32/3)/4 qui fait -32/12 et qui fait -8/3
la limite est égal au coefficient directeur

Oui,

Que peut-on dire de f est de la droite (AB) ?

la droite ab coupe la courbe c de f

Compare le coefficient directeur de la droite et le nombre dérivé de la fonction.

le nombre dérivé est bien 0?

Non, le nombre dérivée est -8/3.

et bien ils sont égaux

Oui

Donc la droite est tangente à la courbe.

d'accord merci beaucoup