DM : calcul algébrique seconde

La figure est formé d'un triangle équilatéral T de côté x, d'un rectangle R, d'un trapèez rectangle P et d'un demi-disque D.

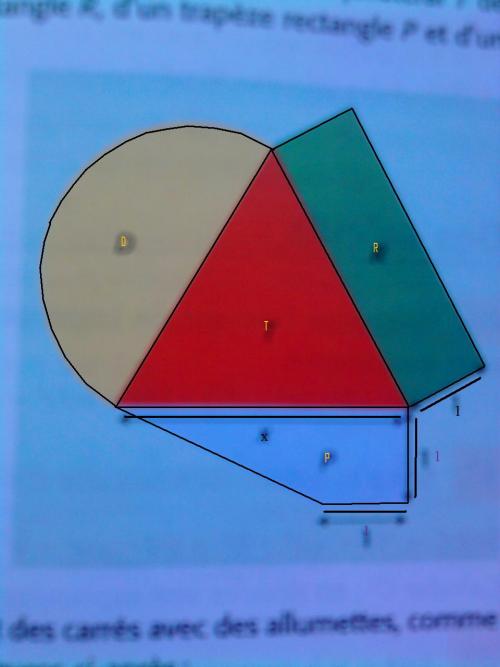
$fichier math$

1.Déterminer, en fonstion de x, les aires respectives de T, R, P et D.

2.Calculer le périmètre de lma figure en fonction de x.

Pouvez-vous me donner des indices pour débuter, les aires n'étant point mon fort, je ne sais pas par quoi commencer.
Merci beaucoup d'avance.

Bonjour,

Indique les formules des différentes aires. Puis remplace les mesures que tu connais.

Bonjour,

Alors -> aire triangle équilatéral : $(B×h)÷2(B\times h) \div 2$
$(x×h)÷2(x\times h) \div 2$
-> aire rectangle : $\times l$
$x×1x\times 1$
-> aire trapèze rectangle : $[(B+b)×h]÷2[(B+b)\times h] \div 2$
$[(x+1)×1]÷2[(x+1)\times 1]\div 2$
-> aire d'un demi-disque : $(π×R2)÷2(\pi\times R^2)\div 2$
$[π×(x÷2)2]÷2[\pi \times(x\div 2)^2]\div 2$

est-ce juste ?

Tu dois exprimer les aires en fonction de x.
pour le triangle, exprime la hauteur h en fonction de x.
Les autres expressions sont justes.

Alors pour le triangle équilatétal cela me fait $[x×(3÷2)]÷2[x\times( \sqrt{3}\div 2)]\div 2$
non ?

C'est x²√3/4

Merci donc en résumé on a :
-> triangle équilatéral : x²√3/4
-> rectangle : x*1
-> trapèze rectangle : [(x+1)\times 1]\div 2
-> demi-disque : [\pi \times(x\div 2)^2]\div 2

Mais maintenant je fais comment pour calculer les aires ? ...

On ne demande pas de calculer mais de déterminer les aires en fonction de x.
Tu as répondu à la question 1.

Passe à la question 2.

Ah ok ^^ merci

pour trouver le périmètre de la figure je fais comment ? je cherche le périmètre de toutes les figures ?

Non,

Pour le périmètre, tu calcules la longueur du pourtour de la figure.

Alors j'ai commencer en haut du rectangle et ca me fait 1+x+1+1+1, mais je bloque pour le côté du trapèze et pour le demi-cercle ...

Trace un triangle rectangle dans le trapèze et calcule l'hypoténuse.

Le périmètre d'un cercle ?

2 * "pi" * rayon et on le divise par 2, je viens de m'en souvenir, désolé

pour le triangle rectangle ca nous fait :

h² = 1² + (x-1)²
h² = x² -2x +2
h = √x² -2x +2

c'est ca ?

C'est juste.

et pour le demi cercle c'est juste aussi ? (2 * "pi" * rayon) et on le divise par 2

Oui

c'est juste aussi pour le demi cercle.

Donc maintenant il faut tout ajouté, ce qui nous fait 1+x+1+1+1+ (√x²-2x+2) + [2 $p i$ *(x/2)]/2

c'est ca ?...

c'est juste ?

Oui,

Simplifie l'expression.

x+4+(x√2x+2)+[2 $p i$ (x/2)]/2

je vois comment la simplifier plus ...

Non
1+x+1+1+1+ √(x²-2x+2) + [2π*(x/2)]/2
= 4 + x + √(x²-2x+2) + π*x/2

ah merci
l'exercice est fini là non ?

Oui, l'exercice est fini.

merci beaucoup pour votre aide
bonne soirée