Construire un arbre pondéré traduisant la situation et calculer les probabilités
-
Ffany97 dernière édition par Hind
Bonjour
exo que je n'arrive pa a faire
On estime à 0,02 la proportion de pièces défectueuses parmi les pièces produites par une usine. Une machine fiable à 99% permet de tester si une pièce est défectueuese ou non.
On prend une pièce au hasard.
On note A l'évènement la pièce est bonne et B l'évenement la machine considère la pièce bonne
-
Construire un arbre pondéré traduisant la situation
-
Calculer p (B)
3 La machine considère la pièce défectueuse. Quelle est la propabilité à 10 puissance -4 près qu'elle soit vraiment défectueuse?
Merci
-
-
Zorro dernière édition par

Bonjour,
Je te propose cet embryon d'arbre à compléter après avoir interprété les informations données par l'énoncé.
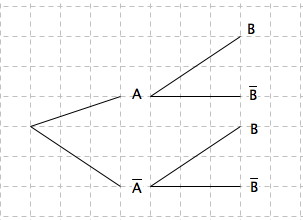
-
Ffany97 dernière édition par
Zorro
Bonjour,Je te propose cet embryon d'arbre à compléter après avoir interprété les informations données par l'énoncé.

oki je vais essayer
-
Ffany97 dernière édition par
je c pas repondre en fesant l'arbre j'ai pa de logiciel
-
Bonjour,
Il n'est pas nécessaire d'avoir un logiciel pour indiquer les différentes probabilités de l'arbre donné par Zorro.
P(A) = ...
-
Zorro dernière édition par

En effet pas besoin de logiciel pour dire ce que tu mettrais à la place de
P(A) ; p(aˉ)p(\bar{a})p(aˉ) ;
pa(b)p_a(b)pa(b) ; pa(bˉ)p_a(\bar{b})pa(bˉ) ;
paˉ(b)p_{\bar{a}}(b)paˉ(b) ; paˉ(bˉ)p_{\bar{a}}(\bar{b})paˉ(bˉ) ;
dans :
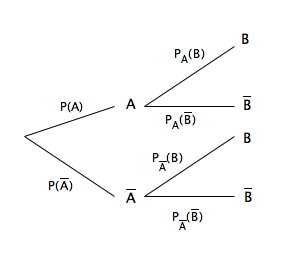
-
Ssil2b dernière édition par
bonsoir, j'ai le meme exo.
est ce que l'arbe est corecte et complet ?
-
Zorro dernière édition par

Non il n'est pas correct ! Je fais des erreurs pour tromper tout le monde ! C'est bien connu qu'ici les modérateurs font des fautes volontairement !
Et puis comme tu les vois il y a partout les bonnes valeurs bien écrites clairement sur chaque branche de cet arbre !
T'es un comique toi !
-
Ssil2b dernière édition par
sil2b
bonsoir, j'ai le meme exo.est ce que l'arbe est corecte et complet ?
en aucun cas j'ai dis que ton arbre était faux et que les modérateurs écrivaient des truc faux. de plus je n'ai pas voulu te vexer mais bon ca serait bien qu'on parle de l'exo si tu est d'accord. merci
-
Zorro dernière édition par

Je vais donc répéter ce que j'ai écrit :
J'ai proposé un embryon d'arbre à compléter après avoir interprété les informations données par l'énoncé.
Par quoi remplacer les probas écrites sur les branches ?
-
Ssil2b dernière édition par
pour commencer,
p(A)=1-0,02
=0.98p(A barre)= 0,02
après je sais pas trop si c'est çà, les probas ça n'est pas évident pour moi.
-
Bonsoir,
C'est juste. Calcule les probabilités des autres branches.
-
Ffany97 dernière édition par
j'ai trouver pour la question 1 et 2
mais la 3 me pose probleme??MERCI
-
Zorro dernière édition par

Qu'as tu trouvé à mettre comme probas sur les branches ?
Pour la 3 ) on te demande la proba de quoi sachant quoi ?
-
Ssil2b dernière édition par
oui, je voudrais bien savoir ce que tu as trouvé pour les autres proba de l'arbre
-
Zorro dernière édition par

Au lieu d'attendre la réponse , ne pourrais tu pas essayer de traduire en proba la phrase :
Une machine fiable à 99% permet de tester si une pièce est défectueuse ou non.
-
Ssil2b dernière édition par
Zorro
Au lieu d'attendre la réponse , ne pourrais tu pas essayer de traduire en proba la phrase :Une machine fiable à 99% permet de tester si une pièce est défectueuse ou non.
j'essaye, j'avais déja donné les 2 premières un peu plus bas
-
Ffany97 dernière édition par
J'ai trouvé l'arbre et la question 2
mais pr la 3 tu px m'aider stp
merci
-
Ssil2b dernière édition par
PAP_APA(B)= [p(B)xp(A)]/p(A) mais p(B) il demande de la calculer après
-
Ffany97 dernière édition par
oui g trouver
-
Ssil2b dernière édition par
en ce qui me concerne, je suis à la 1ère question là. j'ai trouvé que p(A) et p(A bar).
-
Zorro dernière édition par

Alors essayons de décortiquer cette phrase :
Une machine fiable à 99% permet de tester si une pièce est défectueuse ou non.
a) Si la pièce est bonne, quelle est la probabilité que la machine la détecte comme bonne ?
Donc P?P_?P? (??) = quoi ?b) Si la pièce est défectueuse, quelle est la probabilité que la machine la détecte comme défectueuse ?
Donc P?P_?P? (??) = quoi ?Et pour la 3) on te demande : ""La machine considère la pièce défectueuse. Quelle est la probabilité qu'elle soit vraiment défectueuse ?""
Ce n'est pas ce que tu indiques comme calcul qu'il faut faire !
-
Ssil2b dernière édition par
Zorro
Alors essayons de décortiquer cette phrase :Une machine fiable à 99% permet de tester si une pièce est défectueuse ou non.
a) Si la pièce est bonne, quelle est la probabilité que la machine la détecte comme bonne ?
Donc P?P_?P? (??) = quoi ?b) Si la pièce est défectueuse, quelle est la probabilité que la machine la détecte comme défectueuse ?
Donc P?P_?P? (??) = quoi ?Et pour la 3) on te demande : ""La machine considère la pièce défectueuse. Quelle est la probabilité qu'elle soit vraiment défectueuse ?""
Ce n'est pas ce que tu indiques comme calcul qu'il faut faire !
a) pBp_BpB(A)
b)pBb)p_Bb)pB(A bar)
-
Zorro dernière édition par

pBp_BpB(A) c'est la probabilité que la pièce soit bonne si la machine la détectée comme bonne !
Je te demande : Si la pièce est bonne, quelle est la probabilité que la machine la détecte comme bonne ?
PtrucP_{truc}Ptruc (machin) = Proba que machin se réalise si truc est vrai !!!
-
Ssil2b dernière édition par
Zorro
p_B$(A) c'est la probabilité que la pièce soit bonne si la machine la détectée comme bonne !Je te demande : Si la pièce est bonne, quelle est la probabilité que la machine la détecte comme bonne ?
PtrucP_{truc}Ptruc (machin) = Proba que machin se réalise si truc est vrai !!!
pBbarp_{B bar}pBbar(A)
-
Zorro dernière édition par

Tu sais lire ?
On note
A l'évènement la pièce est bonne
et
B l'évènement la machine considère la pièce bonneDonc PBbarP_{B bar}PBbar(A) c'est quoi comme proba ?
Pas celle que je te demande ! Et qui est : Si la pièce est bonne, quelle est la probabilité que la machine la détecte comme bonne ?
-
Ssil2b dernière édition par
Zorro
Tu sais lire ?On note
A l'évènement la pièce est bonne
et
B l'évènement la machine considère la pièce bonneDonc PBbarP_{B bar}PBbar(A) c'est quoi comme proba ?
Pas celle que je te demande ! Et qui est : Si la pièce est bonne, quelle est la probabilité que la machine la détecte comme bonne ?
la pièce est bonne c'est bien p(A)
bon après je vois pas trop la différence entre ce que j'ai écrit et ce que tu me demande
-
Ssil2b dernière édition par
c'est pas p0.99p_{0.99}p0.99(A)
-
Zorro dernière édition par

La probabilité que la pièce soit trouvée bonne si elle est détectée comme bonne cela se résume en langage mathématique en
ProbadeˊtecteˊebonneProba_{détectée bonne}Probadeˊtecteˊebonne(la pièce est bonne) = PBP_BPB(A)
Alors sachant que la machine est fiable à 99% que vaut cette PBP_BPB(A) ?
-
Ssil2b dernière édition par
Zorro
La probabilité que la pièce soit trouvée bonne si elle est détectée comme bonne cela se résume en langage mathématique enProbadeˊtecteˊebonneProba_{détectée bonne}Probadeˊtecteˊebonne(la pièce est bonne) = PBP_BPB(A)
Alors sachant que la machine est fiable à 99% que vaut cette PBP_BPB(A) ?
PB∗0,99P_{B*0,99}PB∗0,99(A)
-
Zorro dernière édition par

Oh lala !!!
Tu traduis comment PB∗0,99P_{B*0,99}PB∗0,99(A) en langage courant ?
Quand on écrit PBP_BPB(A) , dans cette notation A et B sont des évènements !!!
B*0,99 c'est quoi comme genre de bidule ?
-
Ssil2b dernière édition par
Zorro
Oh lala !!!Tu traduis comment PB∗0,99P_{B*0,99}PB∗0,99(A) en langage courant ?
Quand on écrit PBP_BPB(A) , dans cette notation A et B sont des évènements !!!
B*0,99 c'est quoi comme genre de bidule ?
PBP_BPB(A) c'est bien ce que j'ai écrit taleur ??
-
Zorro dernière édition par

Non ... mais c'est pas grave ...
Alors que valent PBP_BPB(A) et PBbarP_{Bbar}PBbar(Abar) ?
-
Zorro dernière édition par

Alors voici la réponse à la première question :
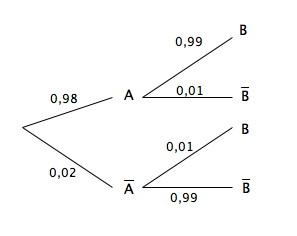
En espérant que tout le monde comprendra pourquoi
PAP_APA(B) = 0,99 et PAbarP_{Abar}PAbar(Bbar) = 0,99 .....
-
Ssil2b dernière édition par
par des calculs détaillé je ne vois pas comment on trouve ces résultats
-
Zorro dernière édition par

sans calcul , juste en lisant et en comprenant l'énoncé , on comprend ;
Une machine fiable à 99% permet de tester si une pièce est défectueuse ou non.
- Cela veut dire que si une pièce est bonne alors la machine la détecte comme bonne avec une proba de 0,99
Cela veut dire que la probabilité que la pièce soit détectée comme bonne (B) sachant qu'elle est bonne (A) est égale à 0,99
Donc PAP_APA(B) = 0,99
- Cela veut dire que si une pièce n'est pas bonne alors la machine la détecte comme pas bonne avec une proba de 0,99
Cela veut dire que la probabilité que la pièce soit détectée comme pas bonne (Bbar) sachant qu'elle n'est pas bonne (Abar) est égale à 0,99
Donc PAbarP_{Abar}PAbar(Bbar) = 0,99
Tu comprends comnent j'ai mis les 0,99 sur les branches ? .....
Je ne sais plus comment t'expliquer autrement !
-
Ssil2b dernière édition par
Zorro
sans calcul , juste en lisant et en comprenant l'énoncé , on comprend ;Une machine fiable à 99% permet de tester si une pièce est défectueuse ou non.
- Cela veut dire que si une pièce est bonne alors la machine la détecte comme bonne avec une proba de 0,99
Cela veut dire que la probabilité que la pièce soit détectée comme bonne (B) sachant qu'elle est bonne (A) est égale à 0,99
Donc PAP_APA(B) = 0,99
- Cela veut dire que si une pièce n'est pas bonne alors la machine la détecte comme pas bonne avec une proba de 0,99
Cela veut dire que la probabilité que la pièce soit détectée comme pas bonne (Bbar) sachant qu'elle n'est pas bonne (Abar) est égale à 0,99
Donc PAbarP_{Abar}PAbar(Bbar) = 0,99
Tu comprends comnent j'ai mis les 0,99 sur les branches ? .....
Je ne sais plus comment t'expliquer autrement !
oui j'ai compri. et pour o,o1 comment on l'interprete dans les 2 cas
-
Zorro dernière édition par

P(Dbar) = 1 - P(D) ....
sur les branches partant d'un même point les probas ont une somme égale à 1 ... c'est mal dit mais c'est comme ça que cela se comprend le mieux !
-
Ssil2b dernière édition par
d'accord.
p(B)=0.01*0.99 ?
-
Zorro dernière édition par

Loi des probabilités totales
P(B) = P(A ∩ B) + P(Abar ∩ B) ....
Il faut leire son cours et refaire les exercices faits en classe !