Montrer des égalités et droites perpendiculaires en utilisant les vecteurs

Bonsoir

je suis une élève de seconde, j'ai un DM à faire sur la droite d'Euler dans le triangle, mais je ne comprends rien, si quelqu'un pouvait m'aider ça serait sympa, voici l'énoncé :

Soit ABC un triangle non aplati, A', B' et C' sont les milieux respectifs des segments [BC], [AC], et [AB] et O le centre du cercle circonscrit au triangle ABC.

Soit H le point défini par : OH= OA+OB+OC

1/ a. Montrer successivement que :

AH=2OA' ; BH=2OB' ; CH=2OC'.

b. Montrer successivement que :
(AH) est perpendiculaire à (BC)
(BH) est perpendiculaire à (AC)
(Ch) est perpendiculaire à (AB)

c. Que peut on en déduire pour le point H ?

2/ Soit G le point défini par :

GA+GB+GC= 0

a. Montrer successivement que :

AG = 2/3 AA' ; BG = 2/3 BB' ; CG = 2/3 CC'

**b.**Montrer que, pour tout moint M du plan :

MA+MB+MC =3MG

c. En déduire que OH = 3OG

d. Que peut on en déduire de la question précédente ?

[En caractères gras, on a indiqué les vecteurs. NdZ]

Bonsoir,

Cherche dans le forum de seconde, tu as plusieurs sujet qui traite de la droite d'Euler.
1/ a) Utilise la relation de Chasles.

Bonjour,
A' étant le milieu de [BC], que vaut OB + OC ?
Fais une figure.

Bon on va le faire une bonne fois pour toutes, cet exo récurrent.

Déjà la figure :

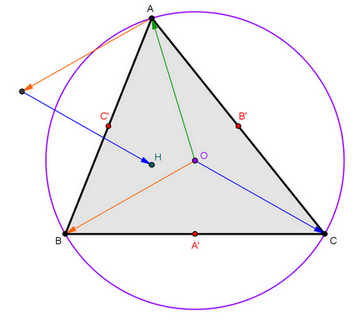
$fichier math$

Citation

1/ a. Montrer successivement que :

AH = 2OA' ; BH= 2 OB' ; CH = 2OC'.

b. Montrer successivement que :
(AH) est perpendiculaire à (BC)
(BH) est perpendiculaire à (AC)
(Ch) est perpendiculaire à (AB)

c. Que peut on en déduire pour le point H ?

a) On sait que OB + OC = 2OA' : c'est la règle du parallélogramme lorsqu'on fait la somme de deux vecteurs de même origine (A' est le milieu de [BC]). Maintenant en soustrayant OA, la définition de H s'écrit OH - OA = OB + OC, d'où AH = 2 OA'.

On procède de même pour les deux autres égalités.

b) On s'appuie sur l'égalité précédente : AH = 2 OA'.
Elle montre que les droites (AH) et (OA') sont parallèles. Or, la droite (OA') est (par construction de O) la médiatrice de [BC]. Ainsi, la droite (AH) est elle-aussi perpendiculaire à la droite (BC).

De même pour les deux autres assertions.

c) Le fait que (AH) et (BC) sont perpendiculaires montre que (AH) est la hauteur issue de A. On en déduit que H est sur chacune" des hauteurs du triangle, c'est donc l'orthocentre de ABC.