3. Fonction carré,inverse, polynome , homographique .

Fonction carré,inverse, polynome , homographique .

  • M

    Je suis perdue , je comprend rien. Et pourtant j'ai cherché...

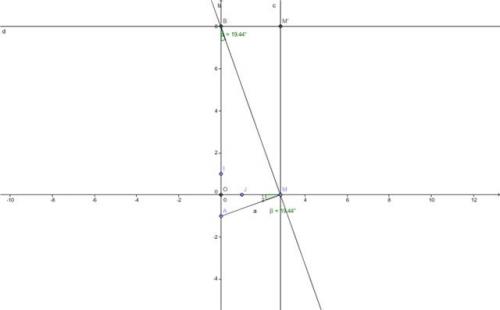
    Dans un repere orthonomé ( O,I,J) , A est le point de coordonées (0;-1). Soit M le point de coordonnées (x;0) où x est un nombre réel. Soit B le point d'intersection de l'axe des ordonées et de la perpendiculaire en M au segment [AM]. Soit M' le point d'intersection de la perpendiculaire en M à l'axe des abscisses et de la perpendiculaire en B à l'axe des ordonées.

    1. Construire la figure ( je l'ai faite avec GeoGebra) , que conjecturer sur la courbe décrite par le point M' lorsque M décrit l'axe des abscisses ?

    2. Que vaut OB lorsque x=0 ?

    3. Supposons dorénavant que x different de 0. Soit a une mesure de l'angle géométrique OBM.

    a) Demontrer que a est aussi une mesure de l'angle géométrique OMA.

    b)Demonter que OM²=OBxOA (calculer tan alfa de deux facons différentes)

    c)En déduire que OB=x² et la courbe decrite par le point M'lorsque x décrit l'ensemble des nombres réels.

    Merci. fichier math

    N 1 réponse
  • N
    Modérateurs

    Bonsoir,

    Quelle conjecture as tu émis ?

    M 1 réponse
  • M

    Voila , J'ai réussi à mettre la figure!

    N 1 réponse
  • N
    Modérateurs

    Quelle courbe décrit le point M ?

    M 1 réponse
  • M

    Mais c'est déjà mon premier probleme. Je comprend pas où doit se trouver la courbe. J'ai réussi tout les exercices que ma prof m'a donné pourtant ils sont du même genre mais celui la je sais pas , je reste bloqué..

    I 1 réponse
  • I

    Bonjour,

    Pour te débloquer en attendant le retour de Noemi ...

    1. Si tu traces plusieurs point M' en prenant par ex pour valeur de x : -3 ; -2 .. jusque 3, tu vas pouvoir conjecturer que M' décrit une para...

    fais quelques points au brouillon.

    1. je te laisse faire

    3a) Dans le triangle ABM, la somme des angles est égale à 180°
    De plus l'angle BAM^ = OAM^
    Exprime la valeur de OAM^ en fonction de a

    Dans le triangle AOM, la somme des angles est égale à 180°
    Exprime OMA^

    3b) Exprime tan(a) dans le triangle BMO rectangle en O puis dans le triangle AMO rectangle en O

    Tu obtiens une égalité ... pense à faire un produit en croix ensuite

    3c) A partir du résultat précédent : OM²=OBxOA

    tu exprimes OB = .../...

    Or d'après leurs coordonnées, quelle est la valeur de OM ? Quelle est la valeur de OA ? (ce sont des longueurs, donc
    positives!)

    M 1 réponse
  • M

    Haa merci beaucoup , je vais faire ce qui reste à faire même si certaine je ne pense pas trop y arriver !! Je vous les montrerais après. Encore merci 🙂

    M 1 réponse
  • M

    Et dois-je refaire mon graphique , je pense qu'il est faux non ?

    I 1 réponse
  • I

    Il n'est pas très visible mais il me semble correct.

    Néanmoins pour exprimer la conjecture, il te faudra placer plusieurs points M' afin d'esquisser la courbe décrite par les différents points M'

    M 1 réponse
  • M

    1)Lorsque m décrit l'axe des abcisses la courbe décrite oar le point m' semble etre une parabole

    2)Lorsque x=0 ,OB =0

    3)a)Dans un triangle BMA rectangle en M :
    La somme des angles d'un triangle est de 180° donc l'angle A = 180°-90 - l'angle Alpha.
    = 90-180 + Alpha.
    =Alpha.
    Par conséquent ,Alpha est aussi une mesure de l'angle OAM

    b)Dans un triangle OBM ,rectangle en O tan(tangeante) Alpha = OM divisé par BO
    Dans le triangle OAM rectangle en O tan Alpha = 0A divisé par OM
    Par conséquent OM sur OB = OA sur OM
    OM² = OB multiplié par OA

    C) OM2= OB mulptilié par OA
    OB multiplié par OA = OM2
    1 multiplié par OB = OM2
    OB =X2
    La distance OM est X ,la distance OB qui lui ait associé est X2 .Le point M' de coordonnées (X;X2) est sur la courbe représentative de la fonction carré.

Se connecter pour répondre