Démontrer droites parallèles / perpendiculaires dans un parallélépipède
-
Ssil2b dernière édition par Hind
bonjour, j'aurais besoin d'un coup de main pour cet exo. merci.
ABCDEFGH est un parallélépipède rectangle. L'espace est rapporté au repère (A,AB,AD,AE) (en vecteur).
1)Donner une représentation paramétrique de la droite (BI) où I est tel que GI=1/3GH.
2)O est le milieu de [BH]et P le milieu de [BG].
a)Déterminer une représentation paramétrique de la droite [GO].
b)Déterminer une représentation paramétrique de la droite [HP].
c)Déterminer, par le calcul, les coordonnées du point d'intersection S des droites (GO)et (HP). Ce point S est-il sur la droite (BI).Notons D, la droite (BS).
d)Déterminer une équation paramétrique de D.3)Déterminer le point M de D tel que (AM) et D soient perpendiculaires.
4)En déduire la distance de A à la droite D.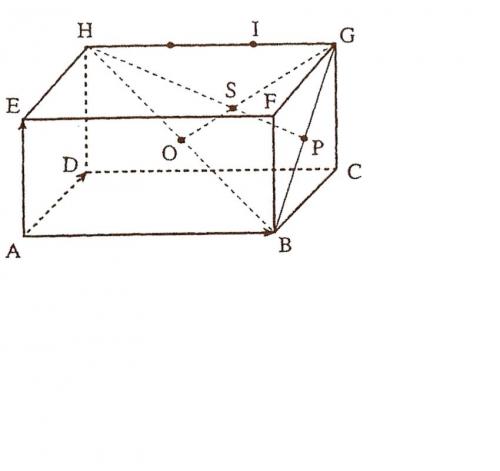
-
Ssil2b dernière édition par
je vraiment du mal à commencer, je n'ai jamais trop su ce qu'était une représentation paramètrique
-
Bonjour,
Cherche les coordonnées des points B et I puis du vecteur BI.
L'équation paramétrique d'une droite qui passe par un point I(xI, yI, ZI) et de vecteur directeur u(a, b, c) s'écrit :
x = xI + ka
y = yI + kb
z = zI + kc
-
Ssil2b dernière édition par
j'ai fati tout les points:
A(0;0;0)
B(1;0;0)
C(1;1;0)
D(0;1;0)
E(0;0;1)
F(1;0;1)
G(1;1;1)
H(0;1;1)I(2/3;1;1) et BI(-1/3;1;1)
-
C'est juste.
Tu peux écrire l'équation paramétrique de la droite (BI).
-
Ssil2b dernière édition par
c'est comme si on place M(x;y;z) sur (BI) et qu'on fait:
BM=k*vect BI ?
-
C'est cela.
-
Ssil2b dernière édition par
plutot t que k.
x=1-(1/3)t
y=t
z=t
-
C'est juste.
-
Ssil2b dernière édition par
2)a) je trouve O(1/2;1/2;1/2) et vect GO(-1/2;-1/2;-1/2) ?
-
C'est juste.
-
Ssil2b dernière édition par
représentation paramétrique de (GO):
x=1-(1/2)t
y=1-(1/2)t
z=1-(1/2)t ??
-
C'est correct.
-
Ssil2b dernière édition par
ok.
2)b) représentation paramétrique de (HP):
x=t
y=1-(1/2)t
z=1-(1/2)t ??
-
C'est juste.
-
Ssil2b dernière édition par
ok.
- je dois calculer les éqations des 2 droites, mais comment je calcule le coefficient directeur dans l'espace ?
-
Pour les coordonnées du point d'intersection, tu fais l'égalité des équations paramétriques.
-
Ssil2b dernière édition par
1-(1/2)t=t
1-(1/2)t=1-(1/2)t
1-(1/2)t=1-(1/2)t ???
-
La première équation te donne la valeur de t.
-
Ssil2b dernière édition par
t=2/3 ?
-
Oui,
Tu en déduis les coordonnées du point d'intersection.
-
Ssil2b dernière édition par
mais je dois remplacer t dans quelles équations ?
-
Dans l'équation de la droite.
-
Ssil2b dernière édition par
je remplace dans l'équation paramétrique de (GO) et (HP) ?
-
De l'une ou l'autre, tu trouveras le même résultat.
-
Ssil2b dernière édition par
S(2/3;2/3;2/3)?
-
Exact
-
Ssil2b dernière édition par
ok mais un truc que je ne comprend pas, comment ça se fait qu'on peut trouver la valeur de t que dans 1-(1/2)t=t ? enfin; dans les 2 autres égalité on trouve 0
-
Pour les deux autres équations, tu trouves 0t = 0, soit toute valeur de R est solution.
-
Ssil2b dernière édition par
2)d) représentation paramétrique de (BS):
x=1-(1/3)t
y=2/3t
z=2/3t ?
-
C'est juste.
-
Ssil2b dernière édition par
2)c) Si S est sur la droite (BI), alors (BI), (HP) et (GO) sont secantes en se même point donc je peux essayer de calculer le point d'intersection entre (BI) et (HP) ou entre (BI) et (GO) et voir si je retrouve S(2/3;2/3;2/3) ?
-
Oui,
C'est une méthode. Tu peux aussi vérifier si les coordonnées du point S vérifient l'équation de la droite (BI).
-
Ssil2b dernière édition par
oui, c'est se que je voulais faire mais je ne sais pas trop comment faire
-
Equation paramétrique de la droite (BI)
x=1-(1/3)t
y=t
z=tPoint S : x = y = z = 2/3
implique t = 2/3
or
2/3 différent de 1-(1/3)x2/3)
Donc le point S .....
-
Ssil2b dernière édition par
ok.
- je n'ai pas trop d'idée à part le produit scalaire, mais il faut déterminer les coordonnées de M donc je penses que ça n'est pas possible
-
Si utilise le produit scalaire.
-
Ssil2b dernière édition par
ok mais j'ai essayé de faire quelque chose mais ça ne mène à rien.
-
Indique les coordonnées des vecteurs BS et AM.
Puis le produit scalaire de ces deux vecteurs.
-
Ssil2b dernière édition par
ça fait : (x-0;y-0;z-0).(-1/3;2/3;2/3)