Déterminer le coefficient directeur de la tangente d'une courbe

bonjour, j'aurais besoin pour cet exo, merci.

On donne dans un repère orthogonal, les courbes C et F représentatives de deux fonctions définies et dérivables sur R. On sait que l’une de ces fonctions est la fonction dérivée de l’autre ; on peut donc les noter g et g'. En outre, ces deux courbes passent par le point J(0;1) et K(-1;0).

a)Associer à chacune des fonctions g et g' sa représentation graphique.
b)Quel est le coefficient directeur de la tangente à C au point d’abscisse 0 ?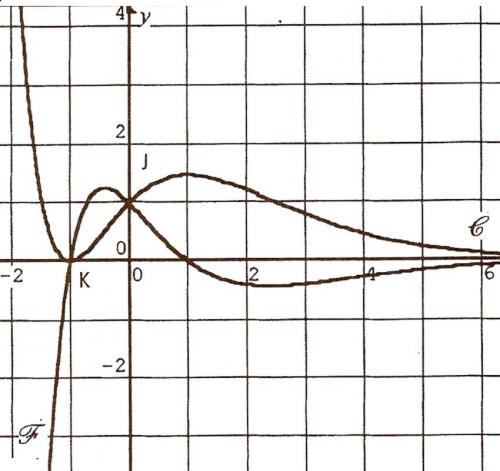

$fichier math$

salut

lorsque la dérivée g' est positive, la fonction g est croissante ; lorsque g' est négative, g est décroissante.

c'est ce qui permet de reconnaître qui est qui sur le graphique.

à toi.

a)
représentation grahique de g: courbe C
représentation grahique de g': courbe F

b) on calcul Yj-Yk/Xj-Xk ?

Bonsoir sil2b

Le coefficient directeur de la tangente est le nombre dérivée soit f'(0).

bonsoir, mais on a pas la fonction

Tu as le graphe, c'est une lecture graphique.

c'est x ?

Cherche sur le graphe la valeur de g'(0).

g'(o)=1

Oui.

ah, c'est donc ça le coefficient directeur

Oui,

Le coefficient directeur de la tangente est le nombre dérivé de la courbe pour l'abscisse du point considéré.

ok. merci, je met un autre exo que j'ai commencé

c'est la suite de cet exo.

partie A : lecture graphique (donc c'est ok)

On donne dans un repère orthogonal, les courbes C et F représentatives de deux fonctions définies et dérivables sur R. On sait que l'une de ces fonctions est la fonction dérivée de l'autre ; on peut donc les noter g et g'. En outre, ces deux courbes passent par le point J(0;1) et K(-1;0).

a)Associer à chacune des fonctions g et g' sa représentation graphique.
b)Quel est le coefficient directeur de la tangente à C au point d'abscisse 0 ?

partie B

Soit l’équation différentielle (E): y'+ y = 2(x+1)e-x

a)Montrer que la fonction f0 définie sur R par:
f0(x)=(x²+2x)e-x est une solution de l'équation (E).

b)Résoudre l’équation différentielle (E') y'+ y = 0.

c)Soit u une solution de (E'). Montrer que f0+u est une solution de (E). On admettra que réciproquement, toute solution f de (E) est de la forme f = f0+u où u est une solution de (E'). En déduire pour x réel, l’expression de f(x)lorsque f est solution de (E).

d)Sachant que la fonction g de la partie A est solution de (E), déterminer g(x) pour x réel.

e)Déterminer la solution h de l’équation (E) dont la représentation graphique admet au point d’abscisse 0 une tangente de coefficient directeur 0.

partie

f est la fonction numérique définie sur R par: f(x)=(x²+2x+2)e-x

1)Étudier les limites de f en + et -.

2)On sait que f est dérivable sur R; déterminer sa fonction dérivée et étudier son signe.
Donner le tableau de variations de f.

3)Dans un repère orthonormal (o;i;j), (unité graphique : 2 cm), on note C' la représentation graphique de f.
a)Déterminer une équation cartésienne de la tangente T à C' au point A d'abscisse -1.
b)Tracer avec soin C' et la tangente T dans le repère orthonormal (o;i;j).

4)a)Déterminer trois réels a, b et c tels que la fonction F définie par F(x)=(ax²+bx+c)e-xsoit une primitive de la fonction f sur R
b) est un réel positif. Calculer en cm² l'aire, A() du domaine compris entre l’axe des abscisses, la courbe C' est les droites d'équation x=0 et x=.

donc, Partie B:

a) j'ai calculé $f_0$ (x)+f' $_0$ (x). je trouve $2(x+1)e^{-x}$ .
b)y'+y=0
y'=-y
solution: $ke^{-x}$
c) je n'y arrive pas

c) Calcule (f0+U)' + (f0+U)= ..

d) Ecrire g(x)

c) je trouve $2(1+x)e^{-x}$ + u

(f0+u)' + (f0+u)=f0' +u ' + f0 + u
= f0' + f0 car u' + u = 0

= $2(x+1)e^{-x}$ d'après a)

pourquoi u'+u=0

Une donnée de l'énoncé : u est une solution de (E')

ah oui. ok.

c) après, il faut en déduire pour x réel, l’expression de f(x)lorsque f est solution de (E).

je ne vois pas comment faire.

g est solution de (E), donc
g = f0 + u

je ne comprend pas cette question.

Pour résoudre une équation différentielle avec second membre, on résout l'équation sans second membre (ici u) puis on cherche une solution particulière (ici f0).
donc la solution de l'équation (E) est f0 + u.
L'énoncé indique de g est aussi solution de l'équation (E)
Donc g = f0 + u
Pour déterminer g tu écris f0 + u
soit g(x) = (x² $2x)e^{-x}$ + $ke^{-x}$
= $e^{-x}$ ( ......)
Tu détermines k à partir d'une donnée de g.

mais c'es la question d ça

Oui c'est d)

La solution de c) est f(x) = (x² $2x)e^{-x}$ + $ke^{-x}$

donc u vaut $ke^{-x}$

Oui,
la solution de y' + y = 0

et f(x)=g(x)

Pour la question d) oui,

Il reste à trouver k.

je veux vraiment être sure.

c) f(x)=(x² $2x)e^{-x}$ + $ke^{-x}$

d)g(x) = (x² $2x)e^{-x}$ + $ke^{-x}$

Oui,

Il reste pour d) à déterminer la constante k.

k=-x²-2x

Non,

Tu utilises un point du graphe, par exemple J (0;1)

et je remplace dans -x²-2x ?

Tu remplaces dans :
g(x) = (x² $2x)e^{-x}$ + $ke^{-x}$

qui est aussi égal à (x² + 2x + $k)e^{-x}$

k=0 ?

Non

g(0) = 1, k = 1 vérifie.

g(o)=k

Oui

g(0) = k et comme sur le graphique on lit g(0) = 1, alors k = 1.

ok. donc g(x)=(x² $2x)e^{-x}$ + $e^{-x}$