Déterminer les dimensions d'un rectangle en étudiant la fonction aire
-
Nnico88s dernière édition par Hind
Bonjours à tous je suis nouveau ici car d'habitude je n'ai pas besoin d'avoir d'aide. Plutot bonne élève mais pas terrible en Math, je suis complètement perdu dans cette partie de mes Exercices
Enoncé: Un maître nageur souhaite délimiter une zone rectangulaire de surveillance sur la mer au bord de la plage. Il possède une corde flottante d'une longueur de 100 m qu'il dispose ainsi:
Excuser moi si le dessin est mal fait)1)Exprimer alors en fonction de x l'aire de la zone en m²
2)Le maître nageur voudrait que cette zone fasse exactement 11,02 ares.
En déduire l'équation traduisant ce voeu3)En utilisant la parabole reprèsentative de la fonction x |-> x² , résoudre graphiquement ce problème.
4)L'aire de la zone de nage peut-elle être égale à 12,5 ares ?
Vous répondrez à cette question de 2 manières:
a) par une argumentation graphique.
b) par une résolution algébrique.Voila le sujet, j'ai fait tous les exercices sauf celui-ci qui devient une torture pour moi avec le nombre d'essaie raté, je n'arrive a rien car c'est un exercice pour l'année prochaine et je n'ai aucun cour la dessus. Pouvez vous m'aidez SvP ? Je remercie d'avance toutes les personnes qui von m'apportez leur aide et un peu de leur temps libre.
-
Bonjour,
La zone est rectangulaire de largeur x.
Quelle est sa longueur ?
-
Nnico88s dernière édition par
Bonjour,
Mon problème vient également de la, on ne me donne pas de donner sur la longueur comment faire... remplacer la longueur par Y ?
Sinon facilement, il faudrait faire Lxl pour trouver cette surface en m² mais la je sèche.
-
Tu connais la longueur de la corde 100 m , donc
.....
-
Nnico88s dernière édition par
Ben X fait 25 m (largeur) et La longueur serait de 50 m ? non
-
Oui, mais c'est un cas particulier.
Dans le cas général :
Si la largeur de la zone de surveillance est x, sa longueur est .....
-
Nnico88s dernière édition par
Ben je dirais que sa longueur est y
-
Oui mais écris y en fonction de x.
-
Nnico88s dernière édition par
Je refais un dessin
Avec CD= bord de plage
Les 3 autres cotés= la corde flottanteOn note AD= x et CD= y
exprimez l'air de la zone:
L'air du rectangle ABCD = AD.CD = x.y (m²)
Je suis à côté de la plaque ?
-
C'est juste, mais tu sais que
DA + AB + BC = 100
soit
x + ......
d'ou
y = ....
-
Nnico88s dernière édition par
y=(100-2x)
Je reporte la valeur dans l'expression de la surface:
x*(100-2x)=..y ?
-
x*(100-2x)= Aire de la surface
-
Nnico88s dernière édition par
Merci voila déjà une question mais je pensse que la suite va être beaucoup plus difficile pour moi :frowning2:
Dans les autres questions je sais que un ares est une unité de mesure de superficie et que un are égale 100 mètres carrés.
Les équations à résoudre c'est pas mon fort mais la il faut la deviner en plus, je ne voie pas du tous.
-
- L'équation :
x*(100-2x)= 1250
à modifier
- L'équation :
-
Nnico88s dernière édition par
Euh sa ne serait pas plutot x*(100-2x) = 1102 ? à la place de 1250 qui serait dans la question 4 plutot ?
-
Exact, c'est bien :
x*(100-2x) = 1102
-
Nnico88s dernière édition par
Pouvez vous m'aider ? les équation et moi ben je n'ai jamais vraiment compris.
Déjà il faut développer la premiere partie ? x*(100-2x)
et passer le 1102 de l'autre côter pour avoir un chiffre nul de l'autre côter ?
-
Oui,
Indique tes calculs.
-
Nnico88s dernière édition par
x*(100-2x)=1102
100x-2x²=1102
100x-2x²-1102=0
x(100-2x-1102)=0
x(-2x-1002)=0
donc x=0 et -2x-1002=0
-2x=1002
x=1002/-2
x=-501Enfin je sais pas trop
-
Les trois premières lignes sont justes.
x*(100-2x)=1102
100x-2x²=1102
100x-2x²-1102=0
tu peux ordonner et diviser par 2
-x² + 50x - 551 = 0 que l'on peut écrire x² - 50x + 551 = 0La résolution est demandée à la question 3, mais graphiquement.
-
Nnico88s dernière édition par
Comment faut-il faire pour résoudre cela graphiquement ?
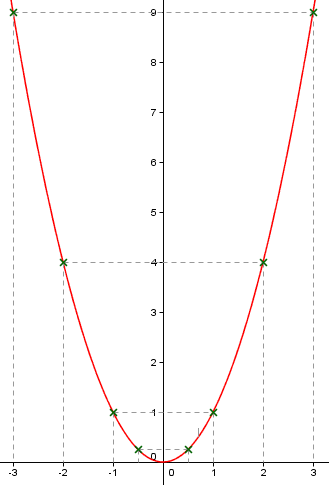
Ceci est la reprèsentation graphique de la fonction x→x² mais après que faire ?
-
Tu dois résoudre :
x² - 50x + 551 = 0
soit
x² = 50x - 551
Donc trace la droite d'équation y = 50x - 551
-
Nnico88s dernière édition par
Donc
x²=50x-551
x²-50x=-551
x-50=-551
x=-551/-50 = 11.02
S={11.02} la droite d'équation est : y= 11.02
C'est sa ?
-
Non,
Trace sur le graphe la droite d'équation : y = 50x - 551
-
Nnico88s dernière édition par
Je n'y arrive pas je suis nul ! j'ai tenter de le faire avec le logiciel géogébra comme indiqué par le professeur mais je sais même pas l'utilisé.


-
Sur géogébra, trace les deux fonctions.
-
Nnico88s dernière édition par
Je suis perdu, sais tu ou on rendre les fonctions dans géogébra?
et les 2 fonctions sont bien:
fonction x→x²
fonction x² = 50x - 551
-
Sur géogébra, tu notes les fonctions dans le cadre à côté de saisie
y = x² et y = 50x - 551
-
Nnico88s dernière édition par
Merci j'ai les 2 fonction
une ressemble à une parabole et l'autre une droite qui coupe la parabole 2 fois.
Que dois je faire maintenant et comment si c'est sur géogébra ?
-
Tu crées un objet dépendant avec la commande intersection avec le nom des deux fonctions.
-
Nnico88s dernière édition par
Ok il ma placé deux point, à chaque fois que les fonctions se coupent
-
Les valeurs de l'abscisse sont les solutions de l'équation.
-
Nnico88s dernière édition par
Je trouve pour etre le plus prècis 16,4 et 36.6
sa pourrait être sa ?
-
Attention, c'est 33,6
Pour une précision au dixième : Oui
-
Nnico88s dernière édition par
ah Oui excusez moi de l'erreur c'est bien 33,6
Donc pour recapituler cette question 3:
Je resous:
x² = 50x - 551
Donc je trace la droite d'équation y = 50x - 551
En tracant les fonction y = x² et y = 50x - 551 je remarque qu'elles se coupent 2 fois. Les valeurs de l'abscisse sont les solutions de l'équation
donc S={16,4;33,6}Pouriez vous m'expliquez entièrement la question 4 avec les fonction a trouver et les calcule à faire.
apres le petit a, pour resolution graphique je pensse qu'il faudra refaire pareil que la dans la question 3 et resolution algébrique sera par le calcule.
-
Question 4)
Refais les calculs avec 1250 à la place de 1102.
-
Nnico88s dernière édition par
Voila j'ai finis l'exercice merci beaucoup de m'avoir vraiment aidé, j'ai passé une journée entier mais aucune importance car c'est le résultat qui compte. Un grand merci car c'est super se que tu fais pour aidé les autres en plus tu enchaines les sujets les un après les autres, en un mot c'est Génial !!
Un Grand Merci et Aurevoir
Cordialement Nico88s.Enfaite j'ai dit aurevoir un peu vite, j'ai un petit doute pour la résolution algébrique de x²=50x-625 comment faire ?
Avec l'argumentation graphique j'ai trouver 25.
-
Jjohn26 dernière édition par
Bonjours à tous, j'avais le même exercice à faire, j'ai très bien compris maintenant merci mais comment on fait avec la résolution algèbrique ?
x²=50x-625
Je ne vois pas par ou commencer cordialement.
-
Pour :
x²=50x-625
cela revient à résoudre :
x²- 50x + 625 = 0Identité remarquable
-
Jjohn26 dernière édition par
Ok Merci donc identité remarquable cela donne:
x²-50x+625=0
x²-2x25+25²=0
(x-25)²=0
C'est bien sa mais après ?