limites et asymptote 1ERE S

Bonjour a tous !! Je n'arrive pas a faire cet exercice pouvez vous m'aidez ??

1.Dans un repere orthonormal (O;i;j) , placez les points A(-2;1) et construisez les droites d et P d'équations respectives x=-1 et y=2. (sa je l'ai fait)

2.f est une fonction homographique telle que : (ax+b)/(x+c) et C sa courbe representative dans le repere (o;i;j).
a) Déterminez a,b et c pour que C passe par A , admette d pour asymptote verticale et P pour asymptote horizontale.

b)Etudiez la fonction F et la construire .

Je n'arrive pas au 2. Je ne sait pas quel demarche entreprendre . pouvez vous m'aidez svp.

salut

i. la courbe de (ax+b)/(x+c) passe par A

cela se traduit par (-2a+b)/(-2+c) = 1

ii. ... admet d pour asymptote verticale

la valeur interdite est -
qqchque tu n'as pas écrit.

iii. y= 2 doit être asymptote horizontale

donc à la limite, (ax+b)/(x+c) tend vers 2 lorsque x tend vers +∞.

essaie d'exploiter cela !

Et pour l'étude je doit faire quoi ?

Bonsoir,

Pour l'étude tu appliques la méthode proposée en cours.
Ensemble de définition, dérivée, sens de variation, tableau de variation ???

je n'arrive pas a determiner a,b et c.Je bloque au niveau des asymptote quelqu'un peut - il me dire ce qu'il faut faire ? je suis perdu ...

salut

la limite de (ax+b)/(x+c) lorsque x tend vers +∞ est égale à a.

Zauctore
salut

la limite de (ax+b)/(x+c) lorsque x tend vers +∞ est égale à a.
C'est pour quel asymptote ?? y=2 ?? et por l'autre asymptote ?

1re S : fais un effort stp

pour l'autre j'en ai déjà parlé : la valeur interdite est -1 (tu l'as rajoutée dans l'énoncé ) ; où peut-on interdire une valeur dans une expression comme (ax+b)/(x+c)

en gros j'ai sa :

1=(-2a+b)/(-2+c)
-1 est une valeur interdite donc c=1 ??
limite de (ax+b)/(x+c) lorsque x tend vers + ∞ est a .( on applique la loi qui dit qu'une fonction rationnelle se comporte comme le monome du plus haut degres du dénominateur et numérateur )
Donc on a a et c et on peut trouvé b . est ce sa ? Mais a on le trouve a partir de quoi ?

j'ai essayé et j'ai trouvé a=2 , b=3 c=1

tu proposes donc (2x+3)(x+1)

c'est bon pour l'asymptote horizontale et pour l'asymptote verticale

et (2(-2)+3)((-2)+1) = 1

c'est donc bon !

ya juste une chose qui m turlupine ^^ quand je tape la fonction sur ma calculatrice je trouve bien une fonction homographique mais les asymptotes sont inversé c'est à dire que x=2 et y=-1 . est ce une erreur de signe quelque part ?

dans l'énoncé c'est bien x=-1 et y=2 que tu veux ?

on obtient bien ceci :

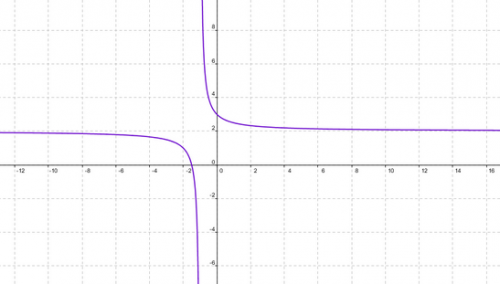
$fichier math$

les axes ne sont pas inversés, ni les asymptotes

mais par le fait que x=-1 par exemple cette droiye ne devrait pas etre parallele à l'axe des abscisse ?

ben non justement : le fait que seulement x soit fixé laisse y libre.

un point de la droite x=-1 a donc une abscisse fixe et une ordonnée variable : il monte et descend sur une droite verticale, c'est-à-dire parallèle à l'axe des ordonnées.

c'est un peu surprenant peut-être au départ, mais toutes les parallèles à l'axe des ordonnées sont les droites "x= constante".

c'est à retenir !

j'ai compris je te remercie pour ta patience

je t'en prie !