résoudre une équation du 3ème degré
-
SSméagol dernière édition par
Bonjour,
J'ai un DNS de mathématiques assez difficile a résoudre :
(E) est l'équation suivante : x³-2x-3=0-
Montrer que 0 n'est pas solution de (E).
Cette question est celle que je ne sais pas résoudre ( la 1) )
-
En déduire que résoudre (E) revient a résoudre l'équation (E1) :
(E1) X²-2=3/x
J'ai trouvé : x(x²-2)-3=0, x(x²-2)=3 Donc on met tout sur x et on trouve le résultat qui est :
x²-2=3/xMerci d'avance pour l'aide.
"La musique est une mathématique sonore, la mathématique une musique silencieuse." [
Edouard Herriot]
-
-
Zauctore dernière édition par

salut
Citation
(E) x³-2x-3 = 0- Montrer que 0 n'est pas solution de (E).
remplace x par 0 dans le membre de gauche de l'équation et vois si c'est égal au membre de droite.
- Montrer que 0 n'est pas solution de (E).
-
SSméagol dernière édition par
Merci,
Désolé, j'ai remarqué ça 10 minutes après avoir posté ce commentaire:rolling_eyes:une autre question est : résoudre x³-x+1=0 .
Or, je ne sais pas comment faire pr qu'il n'y ait plus qu'un x ...
-
Salut,
Je ne connais pas de méthode pour résoudre x²-2=3/x (équivalente x³-x+1=0).
D'après ce que je connais du programme de seconde, je pencherais pour une résolution graphique à partir de la parabole y=x²-2 et de l'hyperbole y=3/x ... c'est une hypothèse.
Tu devrais nous donner ton énoncé complet pour qu'on puisse mieux t'aider.
-
SSméagol dernière édition par
énoncé complet :
(E) x³-2x-3=0
- Montrer que 0 n'est pas solution de (E)
Résolu
- En déduire que résoudre (E) revient à résoudre l'équation (E1) :
(E1) x²-2=3/x
Résolu
- Résoudre graphiquement (E) et (E1) en expliquant la méthode.
Résolu
4)Résoudre x³-x+1=0
à résoudre.
Merci pour votre aide

"L'imagination est plus importante que la connaissance" [A. Einstein]
-
LLind dernière édition par
Sméagol
Salut,Je sais, cette équation est toute simple, mais pourtant je n'arrive pas a la résoudre ...
Si possible, aidez moi
x³-x+1=0
Merci
Bonjour, pas besoin de doubler ton post pour un même exercice !
Contrairement à ce que tu penses, cette équation est loin d'être "toute simple", du moins au niveau seconde.
J'envisagerais à ta place de faire à nouveau appel à la résolution graphique.Commence par mettre x en facteur pour essayer de ressortir une équation de deux fonction de formes connues.
-
OK merci pour l'énoncé complet. J'avais donc vu juste : résolution graphique.
Il faut donc que tu traces les 2 courbes d'équation y=x²-2 et y=3/x.
Les solutions sont les abscisses des points d'intersection entre les 2 courbes.
-
SSméagol dernière édition par
ce que j'ai fait (vers 17 h ^^) est la chose suivante :
x(x²-1)+1=0
x(x-1)(x+1)+1=0
x(x-1)(x+1)=-1et là je bloque ...
je pense même que la dernière ligne est inutile ...
-
Zauctore dernière édition par

salut
arrête l'algèbre, tu n'y arriveras pas de cette façon.
la résolution graphique t'a donné quelle(s) solution(s) ?
-
SSméagol dernière édition par
non ...
je penses qu je me suis trompé, je vais me faire un BON graphique bien précis ^^
dès que j'ai trouvé un résultat, je vous le ferait parvenir
-
Zauctore dernière édition par

ok
-
SSméagol dernière édition par
j'ai trouvé environ -1.31
Merci pour tout votre aide
-
As-tu pensé à vérifier ta solution dans l'équation de départ ?
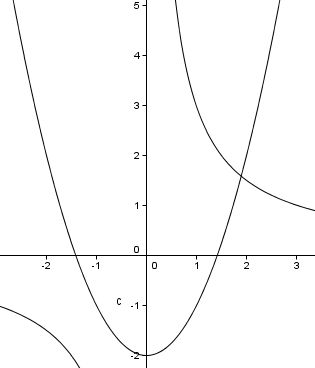
-
SSméagol dernière édition par
oui, et j'ai a peu près la bonne réponse (-1,31+1,31+1=0.061909 environ = 0)
Merci
-
Tu as juste oublié de mettre au cube et de regarder le graphique que je t'ai posté ci-dessus ^^
-
SSméagol dernière édition par
en fait, l'équation est x3x^3x3-x+1.
donc j'ai fais la courbe x2x^2x2-1 et la courbe -1/x