aide: probabilité.

Bonsoir, j'ai quelques dificultés à résoudre cet exercice, un peu d'aide srait la bienvenue, merci d'avance.

Une urne contient 10 boules indiscernables, 5 rouges, 3 jaunes et 2 vertes.
On tire au hasard et simltanément 3 boules de cette urne. Les réponses seront données sous forme de fraction irréductible.

[B]1. soit Ω l'univers associé à cette expérience.
Montrer que le cardinal Ω est égal à 120.

soit les événements suivants:
A "les trois boules sont rouges"
B "les trous boules sont de la même couleur"
C" les trois boules sont chacunes de couleurs différentes"

a)montrer que p(A)= 1/12
b)calculer p(B) et p(C)

on appelle x la variable aléatoire qui à chaque tirage associe le nombre de couleur obtenue. déterminer la loi de probabilité de x et calculer son espérance.

Je n'arrive pas à trouver le cardinal, j'ai trouvé 19 possibilités d'ordre des boules...

pour prouver que p(A)= 1/12, je ne sais pas comment m'y prendre, car comme il y a 5 boules, il y a plusieurs posibilité de tirer 3 boules en sachant qu'elle sont différentes...

Pour P(B), il faut additionner P(A) et celui des boules jaunes, qui est p(J)= 1/120, car il n'y a qu'une possibilité possible.
Pour p(C), c'est l'événement contraire de A, donc p(C)= 1-p(A).

Pour le 3., je ne sais pas.

Bonsoir,

Le cardinal de l'univers correspond à C(3;10) le nombre de combinaison de 3 boules parmi 10.
Combien de choix de 3 boules parmi 5 ?

$10^3$ ?...
il y a 60 chois de 3 boules parmi 5

Non
C(3;10) = 10x9x8/(3x2) = ...

C(3;5) = ....

C(3;10)=120, mais je ne comprends pas pourquoi ces chiffres.

C(3;5)= 60/120 ?

Tu n'as pas appris les notions d'arrangement et de combinaisons ?

a) p(B)= 11/120 et p(C) 11/12

arrangement de combinaisons ? ça ne me dis rien du tout...

Comment calcules tu le nombre de façons de choisir 3 lettres parmi 5 ?

L'espérance de X est égale à 3,8.

Eh bien j'ai ecris moi même le nombre de façon de choisir 3 boules parmi 5 en les nommant: a,b,c,d,e. en commençant par la boule a, j'ai trouvé 12 hoix de choisir 3 boules parmis les 5, et j'ai fais 12*5 pour le nombre de boules. C'est faux ?

En fait,
pour choisir la première boule 5 choix
la deuxième 4 choix
la troisième 3 choix,
Donc 5x4x3 = 60

ah d'accord.
Mais la p(A) que j'ai trouvé est fausse... pourtant c'est le nombre de cas favorables / le nombre de cas possibles pour trouver la probabilité ...

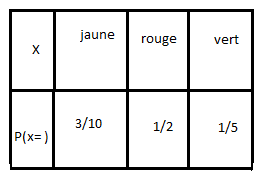
$fichier math$

tableau de la loi de la probabilité.

60 correspond au nombre de chois possibles de 3 objets parmi 5, on considère qu'ils sont discernables,
or les boules sont indiscernables, donc il faut diviser ce nombre par le nombre de choix possibles de 3 boules parmi 3, soit 3x2 = 6
On trouve donc 60/6 = 10 possibilités donc P(A) = 10/120 = ...

donc p(A)= 10/120= 1/12.

b) p(B)= 11/120 et p(C) 11/12
L'espérance de X est égale à 3,8.

P(C) est faux.

Bonne nuit.

D'accord, merci et bonne nuit.