Etudier une fonction et donner son tracé
-
Ppeace dernière édition par Hind
Bonjour, voici un exercice que je n'arrive pas à finir, de l'aide serait la bienvenue
 merci d'avance.
merci d'avance.
Donc voilà:Soit la fonction f définie sur R par f(x)= (x-1)²-4.
Ci dessous sa représentation graphique, notée C, dans un repère orthonormé.Partie A
- Résoudre l'équation f(x)=0. Interpréter graphiquement les réponses obtenues.
- Justifier, par calculs, que, pour tout réel x, f(x)> ou égal à f(1).
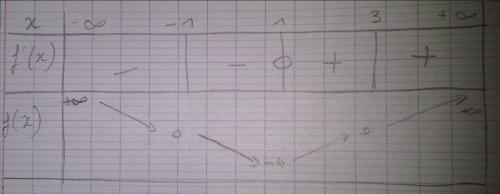
- Étudier les variations de la fonction f.
- Vrai ou faux: « a>ou égal b => f(a) > ou égal f(b) »? justifier votre réponse.
- Justifier que lim [f(x)-f(3)]/x-3 quand x->3 =4.
Partie B
Tracer, sans justification, en couleur, dans le repère précédent, la représentation graphique C' de la fonction g définie sur R par g(x)=|f(x)|.Partie C
Soit la fonction h définie sur R-{3} par h(x)= (x+1)/(x-3)
1.a) Démontrer que h(x)=f(x) <=> x3x^3x3-5x²+2x+8=0
b) Déterminer trois réels a,b,c tels que, pour tout réels x, x3x^3x3-5x²+2x+8= (x-4)(ax²+bx+c).
c) Résoudre l'équation h(x)=f(x).
2.Démontrer qu'il n'existe pas de réels a,b,c tel que, pour tout réels x, x3x^3x3-5x²+2x+8=(x-1)(ax²+bx+c)A1: je trouve x= -1 et x=3. Sur le graphique on remarque que la courbe passe par 0 pour x=3 et x=-1.
-
f(1)= -4. f(x)=(x-1)²+(-4) => f(x)= (x-1)²+f(1). Donc f(x)> ou égal f(1).
-
f'(x)= 2x-2
j'ai réussi à démontrer le C1a).
Pour le reste je suis coincée.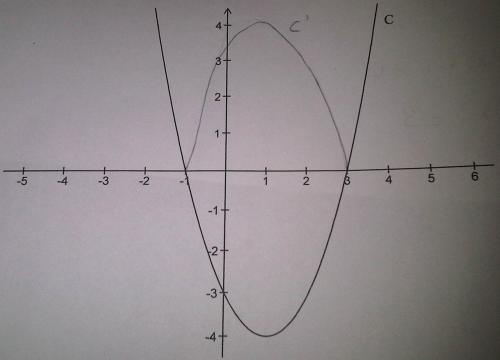
-
Bonjour peace,
Tes trois premières réponses sont justes, qu'est-ce qui te bloque exactement pour la suite ?
Pour le A-4), est-ce vrai ou faux à ton avis ?
Pour le A-5), la formule utilisée devrait te rappeler une formule de cours !
Pour le B c'est ok, pour le C-1)b), tu peux développer (x-4)(ax²+bx+c) et identifier ensuite les coefficients de chaque puissance de x pour retrouver x3x^3x3-5x²+2x+8, ça te permettra de trouver a, b et c.
Pour le C-1)c), il faut réutiliser les questions a) et b).
Pour le C-2), tu peux évaluer chaque membre de l'équation en une valeur particulière.N'hésite pas à détailler tes questions !
-
Ppeace dernière édition par
Eh bien pour le A-4, c'est faux: si on prend -1 et 3, 3>1, pourtant (f(-1)=f(3).
Pour le A-5, je ne m'en souviens pas

Pour le C-1 b) j'ai trouvé a=1 b=-1 et c=-2.
Pour le C-1 c) j'ai essayé plusieurs fois de résoudre l'équation mais je n'y arrive pas...
Pour le C-2 j'ai trouvé a=1 b=-4 et c=-2. J'ai pris comme valeur x=2. Lorsque je remplace les valeurs, je ne trouve pas le même résultat je trouve à gauche 0 et à droite -6.
-
C'est ok pour la A-4
Pour la A-5 en fait je ne suis pas convaincu de ce que je t'ai avancé... Est-ce que tu sais ce qu'est un taux de variation ?
Pour le C-1)b) c'est ok
Pour le C-1)c), résoudre l'équation qu'on te donne revient à résoudre une autre équation, d'après le C-1)a). Et grâce au C-1)b) tu peux exprimer cette équation légèrement différemment... Enfin, un produit est nul, si l'un de ses facteurs au moins est nul...
Pour le C-2), tu ne peux pas trouver de coefficients pour cette équation, les coefficients que tu as déterminé ne collent pas, mais ce n'est pas vraiment une preuve que ça ne marche pas. Tu peux évaluer les deux membres, mêmes sans avoir les coefficients en une valeur particulière, vois-tu laquelle ?