Calculer une aire en utilisant une primitive
-
HHypoxia dernière édition par Hind
Bonjour, je ne me souviens plus du tout comment faire un calcul de primitive ou d'intégale... mon bac remonte à très loin et je suis un petit peu perdue
J'ai besoin de votre aide s'il vous plaitVoici le graphique:
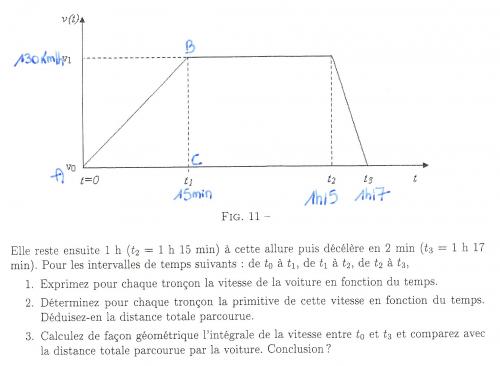
A t0, v(t) = 0 km/h
A t1, v(t) = 130 km/h
A t2, v(t) = 130 km/h
A t3, v(t) = 0 km/hPour la question 3 je pense qu'il faudra calculer l'air de chaque partie de la courbe au dessus de l'axe des abscisses.
Mais j'ai besoin d'aide pour démarrer la question 2Merci beaucoup
-
Mmathtous dernière édition par
Bonjour,
La primitive d'une fonction constante est une fonction de la forme ax + b, puisque la dérivée d'une telle fonction est a.
Il faut donc, pour chaque tronçon, déterminer a et b.
Cela se fait en regardant les valeurs particulières ( aux bornes ici ).
-
HHypoxia dernière édition par
v(t) = at + b
De t0 à t1: a=0 et b=1/4h v(t) = 1/4h
De t1 à t2: a=1/4h et b=1h15 v(t) = 1/4ht + 1h15
De t2 à t3:a=1h15 et b=1h17 v(t) = 1h15t + 1h17Ai-je compris ou bien pas du tout?
Merci pour votre aide
-
Mmathtous dernière édition par
De t0 à t1 : c'est le contraire :
v(0)=0 donc b=0 et v(1/4) = 130 donc a = ...
Précise avant de commencer que tu choisis l'heure ( tu peux aussi choisir la minute ) pour unité de temps. Ainsi, tu n'as pas à écrire h après tes durées.Corrige puis fais de même pour les autres tronçons.
-
Mmathtous dernière édition par
Je vais déjeuner.
A+
-
HHypoxia dernière édition par
De t0 à t1 (en h)
v(0) = 0 donc a=0 et b=0
v(1/4) = 130 donc a=1/4 et b=130De t1 à t2
v(1/4) = 130 donc a=1/4 et b=130
v(1,15) = 130 donc a=1,15 et b=130De t2 à t3
v(1,15) = 130 donc a=1,15 et b=130
v(1,17) = 0 donc a=1,17 et b=0Ensuite pour en déduire la distance totale parcourue
Je sais le faire de t1 à t2 = 130 km en une heure
Mais comment faire pour l'intervalle t0 à t1 avec la vitesse qui augmente?
Merci bcp
-
Mmathtous dernière édition par
Non ce n'est pas cela.
De t0 à t1 : v(t) = at +b
Si t = 0 : v(0) = a0 + b = b
Or, v(0) = 0 ( graphique ), donc b=0
Si t = 1/4 ( en heures ) : v(1/4) = a1/4 + 0 ( b = 0)
Or v(1/4) = 130 ( graphique.
Donc 130 = a1/4 , donc a = 1304 = 520
En conclusion, v(t) = 520t + 0 = 520t.Fais de même pour les deux autres tronçons.
-
HHypoxia dernière édition par
D'accord...
donc de t1 à t2Pour t1: v(t)= 520t (comme précédemment)
Pour t2:
si t=5/4 (de heures): v(5/4) = a5/4 + 0 (b=0)
or v(5/4) = 130 (graphique)
Donc 130 = a5/4, donc a = (130*4)/5 = 104
En conclusion, v(t) = 104t
-
Mmathtous dernière édition par
Non
v(t) = at + b MAIS avec des a et b différents des précédents ( éventuellement ).
v(t1) = v(1/4) = ? c'est une valeur numérique que tu lis sur le graphique, ce n'est pas une fonction de t comme ce que tu as écrit ( 520t ).Alors : v(t1) = v(1/4) = ?
v(t2) = v(5/4) = 130 : cela est juste.
-
HHypoxia dernière édition par
d'accod
v(t1) = v(1/4) = 130 (graphiquement)
v(t2) = v(5/4) = 130 (graphiquement)v(t3) = v(77) (en min) = a*77 + b
Or v(t3) = 0 (graphiquement)
donc a = 0 et b = 0
-
Mmathtous dernière édition par
Attends : une chose à la fois .
Tu n'as pas terminé le second intervalle.
Citation
v(t1) = v(1/4) = 130 (graphiquement)
v(t2) = v(5/4) = 130 (graphiquement)oui, mais maintenant calcule le a et le b correspondants.
-
HHypoxia dernière édition par
v(1/4) (heures) = a1/4 + b avec b=0 (précédemment calculé par vous)
v(1/4) = 130 (graphiquement)
a1/4 + b = 130
a*1/4 = 130
a = 520
donc v(1/4) = 520tv(5/4) (heures) = a5/4 + b avec b=0
v(5/4) = 130 (graphiquement)
a5/4 + b = 130
a*5/4 = 130
a = 104
donc v(5/4) = 104tEn fait je ne suis pas sure du tout du b=0... il a été calculé précédemment donc il garde la même valeur????
-
Mmathtous dernière édition par
Non : b=0 c'était pour le premier intervalle,
pas pour le second.
Reprends pour le second intervalle :
v(1/4) = 130
v(5/4) = 130
v(t) = at + b
Donc v(1/4) = 130 donne a*(1/4) + b = 130
Et v(5/4) = 130 donne a*(5/4) + b = 130Avec ces deux équations tu peux calculer a et b.
Montre tes résultats, on s'occupera du troisième intervalle plus tard.
-
HHypoxia dernière édition par
D'accord donc j'ai fait un système et je trouve a=0 et b=130
-
Mmathtous dernière édition par
Oui.
Donc, pour le second intervalle : v(t) = 0t + 130 = 130 ( fonction constante comme cela se voit sur le dessin ).
-
HHypoxia dernière édition par
D'accord oui tout s'éclaire
De t2 à t3
v(t) = at + b
v(t2) = v(75) (minutes) = 13/6 (graphiquement) (j'ai converti en km/min)75*a + b = 13/6
v(t3) = v(77) (minutes) = 0 (graphiquement)
77*a + b = 0
Je résouds le système et je trouve a = -13/12 et b = 1001/12 (je n'ai pas réussi à simplifier...)
v(t en min) = -13/12t + 1001/12 car fonction décroissante
-
Mmathtous dernière édition par
Ah non : garde partout les mêmes unités, sinon il y aura incohérence pour les questions suivantes.
Conserve les km et les heures ( tant pis : ç'aurait été plus simple en km et min ).
Récris tes équations.
Le raisonnement cette fois me paraît juste.
-
HHypoxia dernière édition par
v(5/4) = 130 (graphiquement)
5/4*a + b = 130v(77/60) (heures) = 0 (graphiquement)
77/60*a + b = 0Je trouve a = -3900 et b = 5005
v(t) = -3900t + 5005
ça me parait logique parce que la voiture freine brusquement...
-
Mmathtous dernière édition par
Les résultats me semblent justes.
Je dois maintenant me déconnecter .
A+