problème de récurrence : nombre de diagonales d'un polygone convexe
-
Zzoe1993 dernière édition par
bonjour, j'ai un problème dans
cette exercice que je n'arrive pas:S
j'espère que quelqu'un pourra m'aiderle nombre n est un entier supérieur ou égal à 3.
Sur un cercle on dispose dans l'ordre n points A1A_1A1, A2A_2A2,... AnA_nAn ; on obtient ainsi les n sommets d'un polygone convexe inscrit dans les cercle.
On note DnD_nDn le nombre de diagonales d'un tel polygone.
1/ En s'aidant d'une figure, donner les valeurs de D3D_3D3, D4D_4D4, D5D_5D5 et D6D_6D6.
2/ Passage de DnD_nDn à Dn+1D_{n+1}Dn+1 ; le polygone à n côtés A1A_1A1, A2A_2A2,... AnA_nAn étant tracé avec ses diagonales, on ajoute un n+1 point B que l'on place sur l'arc [A1[A_1[A1;AnA_nAn] qui ne contient pas de sommet du polygone. En considérant les nouvelle diagonales que le point B permet de construire montrer que Dn+1D_{n+1}Dn+1 = DnD_nDn + n - 1
3/ Conjecturer une expression de DnD_nDn en fonction de n et la démontrer.
merci d'avance
-
Zauctore dernière édition par

Bonsoir
1/ En s'aidant d'une figure, donner les valeurs de D3, D4, D5 et D6.
tu as fait ça ? tout est dans ces premières observations.
-
Zzoe1993 dernière édition par
et ben je pense que D3=D4=D5=D6 ?
-
Zzoe1993 dernière édition par
enfin j'ai fait une figure et je ne suis pas sur du résultat je pense que D3=D4=D5=D6=3
-
Zauctore dernière édition par

certainement pas.
toi, tu n'as pas fait de dessin ou alors pas correct : pas bien pas bien

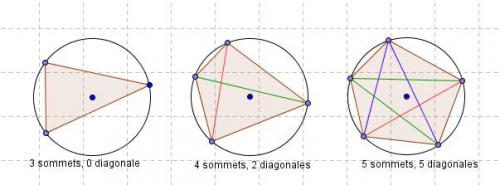
le passage d'une figure à l'autre semble t-il suivre le modèle annoncé à la question 2 ?
c'est-à-dire, est-ce que si l'on ajoute un sommet, le nombre de diagonales augmente du nombre de sommets précédent moins un ? car c'est ce que signifie le Dn+1D_{n+1}Dn+1 = DnD_nDn + n - 1.
-
Zzoe1993 dernière édition par
en passante de la figure 1 à le figure 2 c'est le cas mais de la figure 2 à le figure 3 ce n'est pas le cas
-
Zauctore dernière édition par

Ah bon, 2 n'est pas égal à 0 + 3 - 1 ?
Au fait : je t'ai donné D3D_3D3 = 0, D4D_4D4 = 2 et D6D_6D6 = 5 ; c'est à toi de trouver D6D_6D6 avec une nouvelle figure.
-
Zzoe1993 dernière édition par
ah d'accord j'ai compris!
donc D3=0 D4=2 D5=5 et D6=9
-
Zauctore dernière édition par

ok :
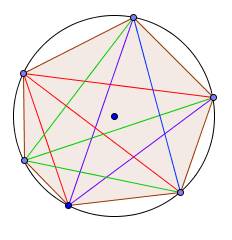
réfléchis à la suite maintenant que tu sembles avoir compris le principe.s'il le faut essaie de dessiner pour trouver D7D_7D7.
-
Zzoe1993 dernière édition par
pour la question 2 il faut dire
D4=D3+3-1
D4=0+3-1=2
D5=D4+4-1
D5=2+4-1=5
D6=D5+5-1
D6=5+5-1=9
donc Dn+1=Dn+n-1 est vérifié
-
Zzoe1993 dernière édition par
mais la question 3 je ne comprend pas trop
-
Bonsoir,
Pour la question 3, tu dois proposer une expression de Dn en fonction de n, puis la démontrer.
-
Zauctore dernière édition par

Re. Voici D7D_7D7
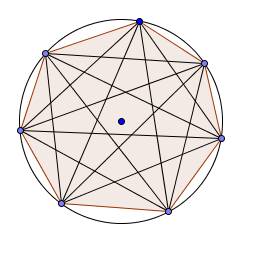
Donc en résumé
$\begin{tabular}{c|c|c|c|c|c|c|c|c} \ \text{nb sommets} & 3 & 4 & 5 & 6 & 7 & \dots & n & n+1 \ \hline \ \text{nb diagonales} & 0 & 2 & 5 & 9 & 14 & \dots & d_n & d_n + n - 1\ \ \end{tabular}$
On sait trouver indirectement le nombre de diagonales, en passant d'une case à l'autre au moyen de la relation de récurrence :
dn+1=dn+n−1d_{n+1} = d_n + n-1dn+1=dn+n−1.
On veut maintenant que tu trouves le passage directdu nombre de sommets n au nombre de diagonales dnd_ndn.C'est la part "conjecture" de la question : il faut deviner en quelque sorte la formule qui donne le nombre de diagonales directement à partir du nombre de sommets.
-
Zzoe1993 dernière édition par
et ben la formule et Dn=-(n-1)+Dn+1 ? et pour la démontrer il faut faire par exemple D4=-4-1+4+1=2 ?
-
Zauctore dernière édition par

Non, tu n'as pas saisi le problème.
La formule dont tu parles dépend de n et de Dn.
Par exemple, pour donner D19D_{19}D19, il faudrait que tu trouves tous les D10D_{10}D10, ..., D18D_{18}D18.Ici, ta/ton prof attend que tu trouves une expression (comme un polynôme en n par exemple) qui permette de calculer D19D_{19}D19 uniquement à partir de l'indice 19 (et sans utiliser la valeur de D18D_{18}D18).
Comprends-tu mieux la question maintenant ?
-
Zzoe1993 dernière édition par
mais si mes réponses 2 et 3 sont juste je ne comprend pas a quoi me sert D7
-
Zzoe1993 dernière édition par
il faut faire un raisonnement par récurrence? car je ne vois pas trop comment parvenir a cette expréssion
-
Zauctore dernière édition par

... à essayer de trouver la formule demandée à la question 3/
Conjecturer une expression de DnD_nDn en fonction de n et la démontrer.
-
Zzoe1993 dernière édition par
je ne comprend pas comment y parvenir
-
Zauctore dernière édition par

D'accord. C'est d'ailleurs là que ça devient intéressant.
Alors il me semble que l'on peut affirmer que ce n'est pas affine en n, par exemple la représentation graphique des premières valeurs de DnD_nDn en fonction de n le montre clairement :
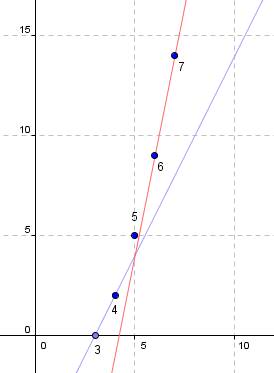
(sinon les points auraient été alignés).Maintenant, il faut regarder du côté du second degré.
Essaie de trouver un polynôme P(n) = an² + bn + c (éventuellement sous la forme factorisée P(n) = (n-u)(n-v) si ça te semble plus facile) tel que :P(3) = 0
P(4) = 2
P(5)= 5
P(6) = 9
P(7) = 14.Fais des essais "intelligents" !
-
Zzoe1993 dernière édition par
j'ai fait pleins de combinaisons mais je n'ai rien trouver j'ai fait
P(4)=(n-2)(n-4)
p(4)=(n-4)(n-4)
p(4)=4n²+4n+2
...
je ne parviens pas au résultat
-
Zauctore dernière édition par

re.
c'est bien !
mais tu n'as pas tenu compte du fait que P(3) = 0, c'est-à-dire qu'il y a un facteur (n-...) n'est-ce pas.
continue !
-
Zzoe1993 dernière édition par
mais les calcul que je vous ai présenté sont un exemple et j'ai utilisé p(4) non p(3)
-
Zzoe1993 dernière édition par
c'est difficile a deviner une expression comme ca
-
Zauctore dernière édition par

re.
Il faut que lorsque n=3 on obtienne la valeur 0 : donc dans le polynôme P(n) il y a nécessairement (n-
...).quel nombre dans les pointillés d'ailleurs ?
un regard sur les figures du début, et tu vois qu'en fait une diagonale concerne *deux *points à chaque fois. Il vaudrait peut-être donc mieux considérer les doubles de DnD_nDn
Vois les valeurs
2P(3) = 0
2P(4) = 4
2P(5)= 10
2P(6) = 18
2P(7) = 28.
-
Zzoe1993 dernière édition par
ben justement je n'arrive pas a trouver la chiffre aprés (n-..)
-
Zauctore dernière édition par

rho : il faut que ça fasse 0 quand n vaut 3
-
Zzoe1993 dernière édition par
(n-0) ?
-
Zauctore dernière édition par

mais non : si tu mets 3 à la place de n, alors (3-0) = 3.
(pardon j'ai un peu traîné)
-
Zzoe1993 dernière édition par
ben c'est (n-3)(n-3)?
-
Zauctore dernière édition par

(n-3) c'est bien
mais est-ce que (n-3)² colle avec les valeurs listées à 19h54 ?
si ce n'est le cas, il faudra que tu ajustes encore le 2e facteur (n-3)(...).
-
Zzoe1993 dernière édition par
non c'est (n-6) ?
-
Zauctore dernière édition par

Non : l'un des facteurs est n-3 ; l'autre est à trouver.
Alors par exemple pour n=4 tu as 2P(4) = 4 c'est-à-dire (4-3)(...) = 4.
De même pour n=5 tu as 2P(5) = 10 c'est-à-dire (5-3)(...) = 10.
Et ainsi de suite.
Je te laisse continuer (car j'ai à faire) - bonne soirée Zoé.
-
Zzoe1993 dernière édition par
ah j'ai enfin trouvé ouffff
alors je résume tout pouvez vous me dire si je ne me trompe pas?question 1:
D3=0 D4=2 D5=5 et D6=9question 2:
D4=D3+3-1
D4=0+3-1=2
D5=D4+4-1
D5=2+4-1=5
D6=D5+5-1
D6=5+5-1=9
donc Dn+1=Dn+n-1 est vérifiéquestion 3:
Dn=(n-3)(n-0)
comme les diagonales concernent 2 points à chaque fois on double les valeurs de Dn
2P(3) = 0
2P(4) = 4
2P(5)= 10
2P(6) = 18
démonstration:
D4=(4-3)(4-0)=4
D5=(5-3)(5-0)=10
D6=(6-3)(6-0)=18
donc Dn=(n-3)(n-0) est vérifiéej'espère que c'est bien ca en tous cas je vous remercie énormément pour votre patience
bonne soirée
-
Zauctore dernière édition par

Attention : c'est 2Dn2D_n2Dn = (n-3)n. Donc DnD_nDn = ...
Car comme tu l'as écrit, on a multiplié par 2 à un moment donné pour mieux voir le phénomène.
Il te reste maintenant à démontrer que cette formule est vrai pour toute valeur de n (car on ne l'a vue que pour les petites valeurs 3 ou 4 ou 5 etc.) et ceci se fait par récurrence - mais je n'ai pas le temps de te guider ce soir !
-
Zzoe1993 dernière édition par
d'accord merci beaucoup