Application de la dérivation pour déterminer les extremums
-
Ttracy dernière édition par Hind
J'ai un exercice que je n'arrive pas à résoudre :
ABC un triangle isocèle en A, et I milieu de [BC] ; M un point de [AI] ; P intersection de (MC) et [AB] ; Q intersection de (BM) et [AC]. Déterminer la position de M sur [AI] pour que la somme des aires de BMC et APMQ soit minimum.
Merci de votre aide.
-
Bonsoir,
L'énoncé est-il complet ? pas de dimensions ?
Exprime les aires des deux polygones.
-
Ttracy dernière édition par
oui l'énoncé est tel quel. L'aire du triangle s'exprime en fonction de x mais pour le quadrilatère, je n'y arrive pas. Il me reste une inconnue.
-
Zauctore dernière édition par

Il faut donc rendre minimum la somme des deux aires colorées (j'ai déjà placé à-peu-près le point M de telle sorte que ce soit le cas sur ma figure).
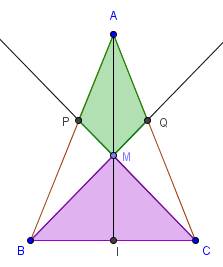
Qu'est-ce que x ? La figure t'est-elle donnée sur quadrillage ?
-
Ttracy dernière édition par
J'ai fait la même figure sur geogebra. J'ai pris x=IM. Il n'y a aucune autre info, ni figure.