placer un point

Bonsoir,
J'ai un exercice à faire, je dois placer un point sur ma figure mais je ne vois pas où. Pouvez vous m'aidez s'il vous plaît ?

Soit H le point défini par vect OH = vect OA + vect OB + vect OC
On sait que G est le centre de gravité, I et J sont les milieux des segments [BC] et [AC] et ABC est inscrit dans le cercle de centre O

Merci d'avance !

$fichier math$

Bonsoir,

Pour placer le point H, tu utilises la relation vectorielle
D'abord vect OA + vect OB = vect OH' puis vect OH' + vect OC = vect OH.

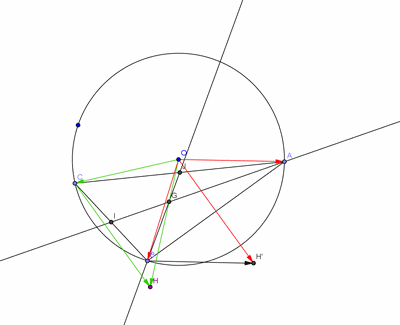
Donc H est là ? $fichier math$

Oui,

H est la.

Il y a une question qui suit dans mon devoir que je n'arrive pas à faire, pouvez vous m'aider ?

Démontrer que vectGB + vectGC = 2 vectGI

Merci d'avance !

Applique la relation de Chasles.

J'ai fait GB + GC = GI + IB GC + IC
= 2.GI + IB + IC

et là je suis bloquée

I est le milieu du segment [BC]
donc vect IB + vect IC = ...

est égale au vecteur nul

Oui, donc tu peux conclure.

okay merci

Est ce que vous pouvez m'aider aussi pour la question 5 ?
Car j'ai utilisé Chasles aussi mais je suis bloquée.
OH = OG + OH
= OG + ?

Quel est l'énoncé de la question 5 ?

Ah oui pardon je croyais l'avoir mise.
Démontrer que OH = 3.OG

Utilise la relation de Chasles à partir de la relation :
vect OH = vect OA + vect OB + vect OC

Je ne vois pas comment, je trouve que vect OH = vecteur nul.

Indique tes calculs. Utilise le point G.

Je viens de refaire le calcul au lieu de partir de OH = OA + OB + OC je suis partie de OH = GA + GB + GC
Mais c'est bon j'ai trouvé maintenant
Merci pour votre aide !!

OH n'est pas égal à GA + GB + GC

J'ai deux dernière questions dont une que j'ai faite mais je ne sais pas si c'est juste.

En utilisant vect AH = 2. vect OI montrer que (AH) est perpendiculaire à (BC). En déduire que (AH) est une hauteur de (BC).
J'ai répondu:
OC = OB et CI = IB donc (OI) est la médiatrice de [CB] donc (CB) et (OI) sont perpendiculaires. vect AH = 2. vect OI c'est à dire que les vecteur AH et OI sont colinéaires donc (AH) et (OI) sont parallèles. Si deux droites sont parallèles, alors toute droite perpendiculaire à l'une et perpendiculaire à l'autre. Donc (CB) est perpendiculaire à (AH).
On en conclut que (AH) est la hauteur de (BC) puisque que (AH) est perpendiculaire à (BC) et elle passe par le sommet opposé, ici A.
(Ma prof m'a dit qu'on pouvait faire beaucoup plus court mais je ne vois pas comment).

9)vect BH = 2. vect OJ déduire que (BH) est une hauteur de ABC.
(là je ne sais pas comment faire)