Toiture à section parabolique et toile de séparation : exo à prise d'initiative

voilà j'ai un exercice à faire mais je ne comprend pas ce qu'il faut trouver,voici l'énoncé:

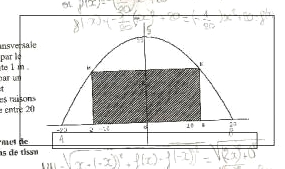
La toiture d'une salle de sport a pour section transversale une arche de parabole dont l'axe vertical passe par le centre de la salle.L'unité sur le dessin représente 1 mètre. On se propose de partager la salle en 2 parties par un rideau de toile vertical MNPQ touchant le sol et suspendu à une poutre horizontale MN. Pour des raisons pratiques, la longueur de la poutre MN ne peut qu'être comprise entre deux valeurs extrêmes : 20m et 30m.
Déterminer la longueur de la poutre qui permet de mettre en place le rideau nécessitant le moins de tissu possible.

En fait, je n'ai pas vraiment réussi à trouver un lien entre la question et un calcul,sachant que mon exercice est sur la récurrence on doit avoir besoin de cette dernière.

J'ai effectué quelque calcul:
-pour l'équation de la parabole j'ai trouvé: y=
-1/(20×²+20)
-j'ai trouvé pour la longueur MN,MN=2× et pour la longueur NP,NP= f(×)
-j'en ai donc déduit l'aire MNPQ, A(mnpq)=[-(1/10)×³+40×]

Je ne sais pas quoi faire avec ça, merci d'avance pour votre aide

$fichier math$

[Edit : modif titre - NdZ]

Bonjour,

Tu étudies les variations de la fonction aire pour déterminer le minimum.

J'ai utilisé la dérivée puis j'ai trouvé pour f(x) (fonction de l'aire)
f(x) décroissante sur ]-∞,racine≈-11.54]
puis croissante sur [≈-11.54,≈11.54]
puis décroissante sur [≈11.54,+∞[

(j'ai marqué les valeurs exactes des racines sur ma feuille)

mais avec cela comment déterminer le minimum?

Vérifie l'équation de la parabole , pour x = 0, y = -1/20 ??

j'ai vérifié avec ces donneés et je trouve bien -1/20=-1/20

Mais sur le graphique pour x = 0, y > 0 non ?

oui y=20 quand x=0, c'est mon calcul de la parabole qui est faux?

C'est l'écriture qui est fausse y = -1/20x² + 20
L'étude des variations est correcte.
Conclus en utilisant les variations.

Est ce que l'équation de la parabole est importante pour l'exercice ou est ce que j'ai juste besoin de l'aire et de ses variations.

Pour les variations, je n'ai pas vraiment compris le but de l'exercice,je sais qu'il faut trouver un minimum,est ce quand la variation de l'aire est au minimum? (c'est à dire quand la courbe est décroissante etqu'elle va repasser croissante?)

Salut,

Citation
Est ce que l'équation de la parabole est importante pour l'exercice ou est ce que j'ai juste besoin de l'aire et de ses variations.
tu as impérativement besoin de l'équation de la parabole pour exprimer l'aire en fonction de x. Et tu l'as fait. Ensuite seule l'aire est à étudier, tu n'as plus besoin de l'éq de la parabole.

Le plus simple je pense est de calculer la demi-aire du rideau, partie de droite pour se limiter à x positif (x = demi-largeur du rideau)

La poutre étant comprise entre 20 et 30m, ça te limite les valeurs possibles de x
10 ≤ x ≤ 15

Tu as trouvé l’équation de la parabole : P(x) = -(1/20)x² + 20

La demi aire du rideau : A(x) = x . P(x) = -(1/20)x³ + 20x
C’est à dire la moitié de l’aire que tu as trouvée

Tu étudies les variations de A : dérivée, valeurs qui annulent la dérivée, signe de la dérivée, tableau de variation de A (tu tombes bien sûr sur la même valeur charnière 20/√3 que tu as déjà trouvée)

C’est à partir du tableau de variation sur [10 ;15] que tu pourras déduire la valeur de x (demi-largeur du rideau) pour laquelle la demi-aire du rideau est mini

Pour conclure, il ne faut pas oublier de multiplier x par deux pour obtenir la longueur de la poutre et de multiplier A(x) par deux pour obtenir l’aire mini.

Citation
Pour les variations, je n'ai pas vraiment compris le but de l'exercice,je sais qu'il faut trouver un minimum,est ce quand la variation de l'aire est au minimum? (c'est à dire quand la courbe est décroissante etqu'elle va repasser croissante?)
Ici, tu ne sera pas dans cette configuration (pas de mini local). Il faut te fier au tableau de variation pour les valeurs possibles de x.

Bonjour, Merci beaucoup pour votre aide,je pense avoir trouver le bon résultat, excusez moi pour le retard mais problème de connexion internet,
Bonne journée