Exercice Géométrie-Fonctions
-
DDunkle dernière édition par
Bonjour,
J'ai un DM à rendre que j'ai presque finis mais je bloque sur le dernier exercice.Dans un quadrilatère APQB.
A tout point A du segment [AB] de longueur 5cm, on associe les triangles équilatéraux AMP et MBQ. On pose AM = x.Je n'arrive pas la première question qui est de justifier que le quadrilatère APQM est un trapèze ainsi que de calculer son aire en fonction de x.
Voila, si quelqu'un peu me donner une piste ce serait sympa, merci.
-
Zauctore dernière édition par

Bonjour
quel genre, le quadrilatère APQB ? c'est pour faire une figure "convenable"...
-
DDunkle dernière édition par
Merci de prêter attention à mon post,
c'est un quadrilatère convexe.
-
Zauctore dernière édition par

Oui ça y est.
Tu aurais dû décrire : soit M sur [AB] ; du même côté de (AB) on construit APM et BMQ équilatéraux ; on considère le quadrilatère (convexe) APBQ.
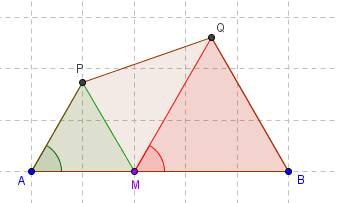
Pour ta question : que vaut l'angle codé ?
-
DDunkle dernière édition par
Oui tu as raison j'aurais pu préciser cela.
Ces angles valent 60° car ils sont dans des triangle équilatéraux.
-
Zauctore dernière édition par

D'où le parallélisme...
-
DDunkle dernière édition par
Désolé je n'ais pas pu répondre avant.
Donc oui, la droite (AB) coupe (AP) et (MQ) en formant des angles complémentaires car on sait que ces angles font tous deux 60°.
Or si un quadrilatère a deux côtés parallèles alors c'est un trapèze.
C'était pas si dur que ça finalement
Sinon pour exprimer l'aire en fonction de x.
On a A = 1/2(b+B)*h
Ce qui donne A = 1/2(x+B)*h, est-ce exact ?
-
Zauctore dernière édition par

attention : angles correspondantségaux, d'où le parallélisme.
pour l'aire : petite base = x, grande base = 5-x n'est-ce pas, mais la hauteur reste à déterminer en fonction de x... utilisation du sinus par exemple.
-
DDunkle dernière édition par
Oui j'avais bien compris que le parallélisme était du à l'égalité des angles correspondants.
Je crois que j'ai réussi à exprimer l'aire du triangle :
Donc on a A = (b+B)/2h. b=x et B = 5-x. Donc on a A = (x-5-X)/2h = 5/2h.
Pour exprimer h en fonction de x, on trace la droite passant par P et perpendiculaire à MQ, on note le point d'intersection R.
Dans le triangle MRP, on a MP=x, PR=h et MR. On connait aussi l'angle M qui est de 120 en faisant 180-(602).
Donc on a sinus m = coté opposé sur hypoténuse = h/x. Donc h = xsin 120.
On en revient à A = 5/2x*sin120.Voila c'est ce que j'ai trouvé, cela me semble correct mais après il va falloir faire des calculs grâce à cette aire que l'on vient d'exprimer et j'ai peur que le sin120 rende les calculs difficiles...
-
Zauctore dernière édition par

Si je peux me permettre, il y a mieux à faire que de prendre sin120 (encore que ça marche : sin120 = √3/2) : tu peux prendre la hauteur issue de P, auquel cas c'est sin60 qui entre en jeu.
-
DDunkle dernière édition par
Mais c'est ce que j'ai fais, j'ai tracé la perpendiculaire à (MQ) passant par par P. Mais je me suis trompé l'angle M est égal à 60 et non 120, je me suis trompé dans le calcul 180-(602)... Mais ça revient au même.
Donc au final on a bien A =x</em>25∗3/2x</em>\frac{2}{5}*\sqrt{3}/2x</em>52∗3/2
-
Zauctore dernière édition par

En effet je n'avais lu ton texte que superficiellement, bloquant sur le 120.
Le fait que le calcul conduise au même résultat tient à ce que deux angles supplémentaires ont le même sinus : sin(a) = sin(180-a), avec a en degrés.
-
DDunkle dernière édition par
Ha oui, je ne comprenais pas pourquoi ça ne changeais pas le résultat...
Merci de m'avoir aidé pour le début de l'exercice, mais j'aimerai bien que tu m'éclaires sur la question suivante.
Il faut calculer l'aire du triangle MPQ en fonction de x. Donc il suffit de calculer l'aire du triangle APM et de la soustraire à l'aire de APQM.
Je trouve que l'aire du triangle APM est x2<em>3/2x^{2}<em>\sqrt{3}/2x2<em>3/2, il me semble que c'est correct.
Donc on a AMPQA_{MPQ}AMPQ = (x</em>52<em>3/2)−(x2</em>3/2)(x</em>\frac{5}{2}<em>\sqrt{3}/2)-(x^{2}</em>\sqrt{3}/2)(x</em>25<em>3/2)−(x2</em>3/2). Mais je n'arrive pas à simplifier cette formule, peut-tu m'aider s'il te plait ?
-
Zauctore dernière édition par

je n'ai pas vérifié tous tes calculs précédents
en factorisant par x² et par √3/2 il te reste 5/2 - 1, soit...
-
DDunkle dernière édition par
Non, en faite je me suis trompé, l'aire du triangle APM est x2∗(3/4)x^{2}*(\sqrt{3}/4)x2∗(3/4), donc on ne peux pas factoriser par 3/2\sqrt{3}/23/2. Je pense qu'en simplifiant on doit trouver une polynôme du second degré car la question suivante est de trouver le maximum et j'obtiens une parabole en rentrant la fonction dans ma calculatrice. Mais je n'arrive toujours pas à simplifier la formule...
-
Zauctore dernière édition par

si, on peut puisque √3/4 = √3/2×1/2
tu as donc x²√3/2(
5/2-1/2) qui est bien un polynôme du second degré.
-
DDunkle dernière édition par
Attend je comprends pas là...
On factorise (x∗52<em>3/2)−(x2</em>3/4)(x*\frac{5}{2}<em>\sqrt{3}/2)-(x^{2}</em>\sqrt{3}/4)(x∗25<em>3/2)−(x2</em>3/4), donc on peut prendre 3/2\sqrt{3}/23/2 comme facteur, ce qui fait (x∗52<em>3/2)−(x2</em>3/2∗12)(x*\frac{5}{2}<em>\sqrt{3}/2)-(x^{2}</em>\sqrt{3}/2*\frac{1}{2})(x∗25<em>3/2)−(x2</em>3/2∗21)
mais il faut prendre aussi xxx et non pas x2x^{2}x2 ??Ce qui donne x3/2∗(52−x−12)x\sqrt{3}/2*(\frac{5}{2}-x-\frac{1}{2})x3/2∗(25−x−21) ?
-
Zauctore dernière édition par

oups pardon tu as raison de protester, j'ai lu trop vite, persuadé qu'il y avait du carré partout ! j'ai vraiment mal lu tes expressions !
x×52×32−x2×34x\times\frac{5}{2}\times\frac{\sqrt{3}}{2}-x^{2}\times\frac{\sqrt{3}}{4}x×25×23−x2×43
donne
34(x×5−x2)\frac{\sqrt3}4\left(x\times5-x^{2}\right)43(x×5−x2)
puis
34x(5−x)\frac{\sqrt3}4x\left(5-x\right)43x(5−x)
c'est mieux comme ça !
-
DDunkle dernière édition par
Ha oui comme ça c'est bon

Je te pose une dernière question puis j'arrête de t'embêter.
Il faut maintenant trouver la position de M (donc x) pour que l'aire du triangle MPQ soit maximale.
Moi je pensais retrouver une formule de type ax2+bx+cax^{2}+bx+cax2+bx+c, et donc j'aurais pu trouver le maximum de la fonction facilement...
En revanche la forme que l'on viens de trouver me laisse un peu perplexe....
-
Zauctore dernière édition par

alors tâche de maximiser 5x-x² !
-
DDunkle dernière édition par
Désolé mais je ne connais pas ce terme... Que veux-tu dire par là ?
-
Zauctore dernière édition par

trouver où a lieu le maximum de la fonction - c'est bien le problème ?
à première vue je dirais pour x = 2,5.
-
DDunkle dernière édition par
Oui c'est ce que je trouve aussi par lecture graphique, mais il faut aussi le démontrer par calcul je pense...
Il faut trouver la position de M pour que l'aire du triangle MPQ soit maximale, donc il faut trouver le maximum de la fonction.
-
DDunkle dernière édition par
Non mais en faite laisse tomber, je dois rendre mon DM demain et je le finirais pas ce soir.
Merci beaucoup pour ton aide, j'y serais pas arrivé tout seul c'est vraiment sympa

-
Zauctore dernière édition par

c'est pourtant simple avec x(5-x) : la courbe est en cloche inversée vers le bas (parabole tournant sa concavité vers les y négatifs), et elle coupe l'axe des abscisses en 0 et 5 ; en conséquence de quoi et pour des raisons de symétrie, son maximum est atteint au milieu de ses racines : (0+5)/2 = 2,5.
sinon, il faut recourir à la forme canonique pour 5x - x² = -(x²-5x).