les axiomes

bonjour, j'ai un devoir maison à faire et je ne comprend pas le premier exercice.
pouvez vous m'aider s'il vous plait à le comprendre?

tout d'abord, on nous donne deux axiomes (que je n'arrive pas très bien a comprendre):

axiome 1: si f est une fonction definie sur une intervalle [a,b] et dont on peut tracer la courbe sans lever le stylo et f(a)<0 et f(b)>0 alors il existe t dans [a,b] tels que f(t)=0.

axiome 2: si f est une fonction definie sur une intervalle [a,b] et dont on peut tracer la courbe sans lever le stylo alors il existe dans [a,b] un nombre qui est un maximum de f sur [a,b] ainsi qu'un nombre qui est un minimum de f sur [a,b]

puis deux questions:

soit f la fonction qui transforme chaque nombre x en x²-2. calculer f(0) et f(5). déduire de l'axiome1 que 0 a un antécédent ou qu'on ne peut pas tracer la courbe f sans lever le stylo. d’après vous peut-on tracer la courbe de f sans lever le stylo? essayer de justifier le mieux possible votre réponse.

je suis totalement dépassée.

Salut,

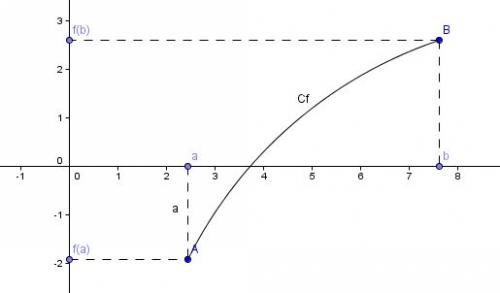
Ci-dessous une courbe Cf représentative de f qui vérifie les conditions de l'axiome 1 (On peut la tracer sans lever le stylo et f(a)<0 et f(b)>0). Saurais-tu placer t sur ce graphique ?

courbe représentative de f

je ne suis pas sur du tout, mais tentons, il serait sur la courbe (ab), comme ordonné 0 et comme abscisse 3.7.

Oui c'est bien ça. Il me semble donc que tu peux comprendre l'axiome 1 qui dit tout simplement que t existe sous les conditions de ma figure.

Tu peux te servir de cette même courbe pour trouver le minimum et le maximum de f sur [a;b] de l'axiome 2.

merci, j'ai compris l'axiome1.

pour l'axiome2, le minimum serait la ou la courbe est la plus basse, c'est à dire le point A (soit (2,4:-2) ) et le maximum la ou la courbe est la plus haute, c'est à dire le point B (soit (7.7; 2.6)) ?

Oui. Mais cette courbe est un cas particulier. On peut imaginer une courbe non monotone dont le sommet serait plus haut que le point B et un "creux" serait plus bas que B.
Bref ce minimum et ce maximum existent toujours sous les conditions de l'axiome 2.

bien, mais je ne vois pas comment avec ces explications, je peux répondre a la question 1.

pouvez vous me l'expliquer s'il vous plait?

Qu'as-tu trouvé pour f(0) et f(5) ?

je suis désolé de répondre si tard, je n'avais plus internet.

par contre, j'ai trouvé 2 pour f(0) et 27 pour f(5).

Re

Tu t'es trompée pour f(0).

je ne vois pas mon erreur:

f(x): x²+2

f(0): 0²+2

f(0): 2

270194

soit f la fonction qui transforme chaque nombre x en x²-2.
270194
je ne vois pas mon erreur : f(x): x²+2
A priori tu t'es trompée aussi pour f(5)

oui effectivement je mal lu mon énoncé.
pour f(0) le résultat serait -2 et pour f(5) le résultat serait 23.

Donc si a=-2 et b=5, es-tu d'accord pour dire qu'une des conditions de l'axiome 1 est vérifiée ?

oui je suis d'accord . mais je ne vois pas comment je pourrais rédiger la réponse?

Quelle l'autre condition de l'axiome 1 ?

l'autre condition de l'axiome 1 est qu' il existe t dans [a,b] tels que f(t)=0.

Non, ça c'est la conclusion.
Une autre condition permet d'arriver à cette conclusion. Laquelle ?

f(a)<0 et f(b)>0? pour -2 et 23 cette condition est bien vérifié.

on peut tracer la courbe sans lever le stylo?

270194
on peut tracer la courbe sans lever le stylo?Oui.

Cette seconde condition peut être vérifiée OU ne pas l'être.

As-tu tous les éléments pour répondre à cette question :
Citation
déduire de l'axiome1 que 0 a un antécédent ou qu'on ne peut pas tracer la courbe f sans lever le stylo