Alignement et vecteurs

Bonjour

J'ai ce devoir à rendre pour le vendredi 22 octobre , j'ai essayé d'appliquer la réciproque du théorème de thalès ou les vecteurs collinéaires, mais je n'y suis pas arriver , et je n'arrive pas à démontrer que les 3 points sont alignés

voici l'exercice :

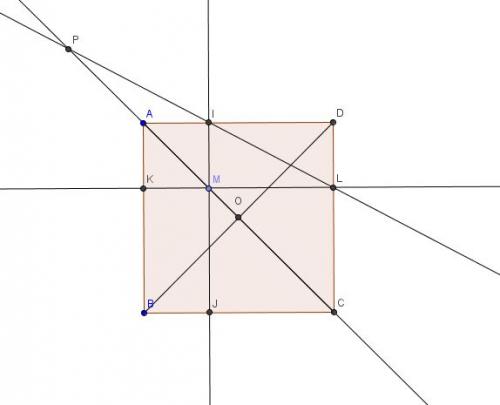
ABCD est un carré de centre O.
M est un point de la diagonale [AC] différent du point O.
La parallèle à (AB) passant par M coupe [AD] en I et [BC] en J.
La parallèle à (AD) passant par M coupe [AB] en K et [DC] en L.
Les droites (IL) et (AC) se coupent en P.
Démontrer que les points K,J et P sont alignés.

Aidez-moi SVP!! :frowning2:
MERCI BEAUCOUP

Bonjour,

vecteurs-alignement-dans-un-carre
hum ...

Plusieurs méthodes sont possibles ...

L'une d'elle consiste à se placer dans le répère (A, AB $→^\rightarrow$ , AD $→^\rightarrow$ ) et de donner des coordonnées variables à M. Explique bien pourquoi son abscisse et son ordonnée sont les mêmes. Ainsi M(m;m) avec m∈IR.

Après avoir déterminé les coordonnées de A, B, C, D tu en déduis celles de I, J, K, L en fonction de m puis celles de P.

Puis enfin les coordonnées de vecteurs pour prouver que J, K, P sont alignés.

As-tu fait le cours sur les repères ?

Bonjours , j'ai le même exercie à faire , et je voudrai savoir comment l'on trouve les coordonnées de P s'il vous plait ?
Merci

Le plus simple à mon avis est de déterminer les équations des droites (IL) et (AC) et de déterminer les coordonnées de leur point d'intersection.

J'y ai pensé , donc pour la droite (AC) se sera : y = x
Mais pour (IL) je ne voit pas , car I , et L varient en fonction de M .

Dans mon post du 20.10.2010, 09:26 je précisai que M a pour coordonnées (m;m) variables. Les points I, J, K, L ont donc aussi des coordonnées qui dépendent de m.

Il faut que tu établisses l'équation de (IL)* en fonction de m*.

Ca pourrait ressembler à : y = f(m).x + g(m) au lieu du y = ax + b habituel.

Donc ça donnerait : y = m*x+m ?

Je ne sais pas mais détaille ton raisonnement et tes calculs si tu veux que je te corrige.

Donc vous me dîte que ce serait du genre ax+b avec y = f(m)x+b

Donc pour b ce sera ym , car I coupe l'axe des ordonnées à la valeur ym
Mais pour ce qui est f(m) je ne voit pas par quoi le remplacer ...

Je suis d'accord pour b, utilise les coordonnées de L pour trouver f(m)...

J'ai saisi l'occasion pour rédiger une math-fiche pour établir l'équation d'une droite :

Déterminer l'équation d'une droite

J'espère qu'elle peut t'aider. Sinon demande ce qui n'est pas clair !

Alors j'ai suivi votre fiche pour l'équation , et je trouve
y(IL) = [(1-ym)/(xm)]
Donc comme P apaprtient à la droite (IL) et (AC) , celui se traduit par
x= [(1-ym)/(xm)]
0= [(1-ym)/(xm)] - x
Et comme il appartient à la droite d'équation y=x
donc P( [(1-ym)/(xm)] - x ; [(1-ym)/(xm)] - x )

Suis je bien partie ?

Merci beaucoup pour votre aide , j'ai réussi a résoudre mon DM et j'ai même eu 20