Trouver la longueur du côté du drapeau en résolvant une équation polynome

Bonjour ,
J'ai un exercice à faire pendant les vacances mais , il me pose assez soucis !
Un drapeau a la forme d'un triangle équilatéral . Il est suspendu par deux de ses coins au sommet de mâts verticaux de 3 et 4 mètre de haut . Le 3eme coin affleure exactement au sol . Quelle est la longueur du côté de ce drapeau ?
Merci beaucoup d'avance pour votre aide , bonne soirée !

salut

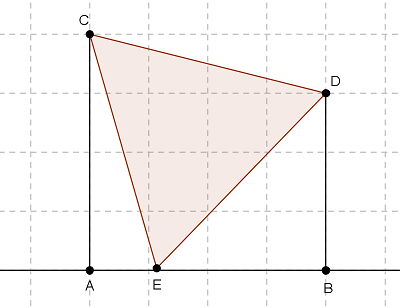
$fichier math$

Re ,
Oh merci pour la figure j'y voit plus clair mais je ne comprend pas quel qoté veulent-ils que je calcule ?

Bonsoir,

Le drapeau a la forme d'un triangle équilatéral donc les trois côtés ont ......
mesure.

Bonjour ,

Ah oui je suis bête ! Les trois cotés ont la même mesure !
Mais cette exercice est dans le chapitre sur les fonctions polynôme et je ne vois pas comment à quoi elles me servent ici ?
Merci !

Exprime la longueur d'un côté en fonction des données.

Connais-tu la mesure de la distance AB ?

Non on ne connait pas la la mesure de la distance AB !
Depuis tout à l'heure je cherche mais je ne vois pas ce que je dois utiliser pour pouvoir exprimer la longueur d'un côté en fonction des données ?
Etant donné que c'est un triangle rectangle on pourrais utiliser le théorème de Pythagore mais j'ai essayer ca ne me mène nulle part je suis vraiment perdu là !
Merci pour vos explications

Si, tu peux utiliser le Théorème de Pythagore.

D'apres le théorème de Pythagore appliqué danq le triangle CAE on a :
CE² =CA²+AE²
CE²=4²+AE²
CE²+16+AE²

et c'est à partir de là que je bloque parce que on ne peut pas dire que CE=√(16+AE²) non ?

Si tu peux écrire cette relation.

Ah d'accord merci , je pensais qu'on pouvait pas!
Maintenant il faut calculer AE je pense mais je ne sais pas comment pourriez vous m'aider s'il vous plait ?

Applique Pythagore dans le triangle DBE.

D'accord .
D'apres le théorème de Pythagore appliqué dans le triangle DBE on a :
DE²=DB²+EB²
DE²=3²+EB²
DE²=9+EB²

DE²=9+EB² donc DE=√(9+EB²)

On se retrouve donc avec deux valeurs du côté d'un triangle mais ensuite je ne vois pas comment on peut faire pour trouver la valeur de AE² et EB² ?
Merci beaucoup

Trace la parallèle à (AB) passant par D, elle coupe la droite (AC) en F.
Utilise Pythagore dans le triangle CDH.

D'apres le théorème de Pythagore appliqué dans le triangle CDH on a :
CD²=FD²+FC²
CD²=1²+FC²
CD²=1+FC²

CD²=1+FC² donc CD=√(1+FD²)

On a réussit exprimer la longueur des côtés en fonction des données mais comment allons-nous faire pour calculer les distances qui nous manque CE , DE et FC .

Merci , vous m'aidez beaucoup !

Tu utilises la relation FD = AE + EB

Je ne vois pas ou vous voulez en venir car par exemples dans 16+AE² on peut remplacer AE par FD-EB ce qui va nous donner 16+(FD-EB)² , mais je ne vois pas à quoi cela nous avance ?

Tu cherches la longueur d'un côté du drapeau. Tu dois trouver une relation en fonction de cette longueur.

Utilise la relation indiquée dans mon précédent mail.

Je pensais faire (16+AE²) - (9+EB²) -(1+FC)² =((FD-EB)²+16)-((FD-AE)²+9)-((AE+EB)²+1 et continuer mais je ne suis pas sure du tout qu'il fasse vraiment faire ca , Cela est-il correct ?

Des relations de Pythagore isole
AE, AE² = CE² - 16 = x² - 16 soit AE =
EB, ...
et
DF, ....

Puis tu utilises le fait que FD = AE + EB

Merci beaucoup apres il suffit de résoudre l'équation x-1=x-4+x-3
et on on trouve x=2 est -ce correct ?
Merci

Merci beaucoup apres il suffit de résoudre l'équation x-1=x-4+x-3
et on on trouve x=2 est -ce correct ?
Merci

Non,

Ce n'est pas la bonne équation, ni la bonne solution.
L'expression comprend des termes avec des racines carrées.

Ah d'accord , Mais la distance de FD n'est-elle pas égale à x-1 , celle de EB à x-3 et celle de AE à x-4 ? :frowning2:

Non,

EB : √(x²-9)

Ah merci je croyais qu'on pouvait réduire un terme pui l'autre aussi séparément , autant pour moi !
maintenant je me retrouve avec √(x²-1)=√(x²-16)+√(x²-9)
Le soucis c'est que je ne comprend pas comment on peut résoudre cette équation ? Pouvons-nous trouver x comme cela ?

Elève ton équation au carré.

D'accord voila ce que cela me donne :
(√x²-1)²=√(x²-16)²+√(x²-9)²
x²-1=x²-16+x²-9
x²-x²+x²=-16-9+1
x²=26
x=√26 ou -√26

Cela est-il correct s'il vous plait ?
Merci beaucoup pour votre aide depuis le début !

Non

c'est :
(√x²-1)²=[√(x²-16)+√(x²-9)]²

D'accord mais peut-on réduire comme je l'avais fais précédemment ? car le premier terme (√x²-1)² donne toujours x²-1 , mais avec l'autre terme [√(x²-16)+√(x²-9)]² je ne m'en sort pas ?
Merci

(√x²-1)²=[√(x²-16)+√(x²-9)]²
x²-1 = x² - 16 + 2√(x²-16)(x²-9) + x² - 9
....

A poursuivre

Pouvez m'expliquer le passage de la premiere a la deuxième ligne s'il vous plait je ne comprend pas tres bien ? Et pouvez-vous aussi m'indiquer au s'arrete la racine carré en mettant des parenthèse ou quoi s'il vous plait ? Merci beaucoup

(√a + √b)² = a + 2V(a×b) + b

(√x²-1)²=[√(x²-16)+√(x²-9)]²
x²-1 = x² - 16 + 2√[(x²-16)(x²-9)] + x² - 9

Ah oui je n'avais pas vu l'identité remarquable avec toutes ces racines j'était perdu , merci !
j'ai effectuer ce calcul :
(√x²-1)²=[√(x²-16)+√(x²-9)]²
x²-1 = x² - 16 + 2√[(x²-16)(x²-9)] + x² - 9
x²-1=x²-16+2√(x puissance 4 -25x²-144) +x² -9
-x²=-24+2√(x puissance 4 - 5x² -144)
J'arrive la et je suis perdu car avec la puissance 4 je ne les jamais vu dans un calcul , pourriez vous m'aider s'il vous plait :frowning2: ?

Une erreur de signe :
-x²=-24+2√(x puissance 4 - 5x² +144)
Soit
24-x²= 2√(x puissance 4 - 5x² +144)
Que tu élèves au carré en précisant que 24 -x² doit être ≥ 0.

Ah oui - et - donne + , autant pour moi !
Par contre une fois que j'ai (24-x²)²=[2√(xpuissance 4 -25x²+144)]²
est-ce que cela doit me donner :
576-xpuissance4=4(xpuissance4-25x²+144)
576-xpuissance4=4xpuissance4-100x²+576
-5xpuissance4=-100x² ,s'il vous plait ?

Non, tu as oublié un terme
(24-x²)²=[2√(xpuissance 4 -25x²+144)]²

576 - 48x² + $x$ ^4 $4(x^4$ -25x²+144)

Ah oui , merci !La je me retrouve avec -52x²=-104xpuissance4 est- ce correct s'il vous plait ?

Non,

vérifie ton calcul.

Oui j'ai mis un 4xpuissance 4 en trop
Maintenant je trouve ca : -52x²=-99xpuissance 4 est-ce possible ?