barycentre et aire

Bonjour voilà j'ai un DM de maths a rendre et le problème c'est que je n'arrive pas et je bloque.
Si vous pouviez m'aider s'il vous plait.

Voila l'énoncé:

Soit ABC un triangle quelconque, et M un point intérieur à ce triangle. On définit alors N milieu de [AM], P milieu de [BN], et Q celui de [PC).

On veut déterminer la position du point M pour que les points M et Q soient confondus.

1/ Ecrire Q comme barycentre de A, M, B, C.
2/ En deduire que: M=Q <=> M est le barycentre des points pondérés A(1), B(1), C(4).
3/ Montrer que, dans ce cas, l'aire du triangle ABC vaut 7 fois celle de MNP.

Merci d'avance pour votre aide!

on sait que N milieu de [AM] P milieu de [BN]
donc N isobarycentre de A et M donc P isobarycentre de B et N
N barycentre de (A;1) (M;1) P barycentre de (B;1) (N;1)

Q milieu de [PC]
donc Q isobarycentre de P et C
Q barycentre de (P;1) (C;1)

Bonjour,

Indique tes éléments de réponse.
1/ Donne l'écriture vectorielle pour le barycentre Q.

1/ G barycentre de (A;1) (M;1) (B;2) (C;4)
je sais pas si c'est sa et comment le démontrer ?

Comment fait-on pour les questions 2 et 3 s'il vous plait ?

Salut,

Q bar {(C;4)(P;4)} et P bar {(B;2)(N;2)} donc par associativité Q bar {(C;4)(B;2)(N;2)}.

Comprends-tu ce que je viens d'écrire ?

bogos13

2/ En deduire que: M=Q <=> M est le barycentre des points pondérés A(1), B(1), C(4).
Vérifie que tu as bien recopié ton énoncé ... j'ai un doute.

Bonsoir, merci de m'avoir répondu.

Non je ne comprend pas trop, pouvez vous m'epliquer ? S'il vous plait.

2/ En deduire que: M=Q <=> M est le barycentre des points pondérés A(1), B(1), C(4).
En effet je me suis trompé sur l'énoncé : c'est M barycentre de (A;1) (B;2)(C;4).
Comment fait-on pour montrer cela ?

Merci d'avance.

Thierry

Q bar {(C;4)(P;4)} et P bar {(B;2)(N;2)} donc par associativité Q bar {(C;4)(B;2)(N;2)}.
J'ai remplacé P dans le 1er barycentre par ce de quoi il est le barycentre. En général on utilise l'associativité dans l'autre sens. Tu saisis ?

Bonjour, merci de m'avoir répondu.

J'ai compri pour la question 1, merci.

Pouvez vous m'expliquer pour les questions 2 et 3 parce que je n'arrve pas. S'il vous plait.

Merci d'avance.

Le fait que Q soit barycentre de A, M, B, C te donne une relation vectorielle (celle de la définition du barycentre).
Dans cette relation, tu remplaces Q par M ...

Bonjour, merci de m'avoir répondu.

J'ai essayé et j'ai trouvé ça :

Q barycentre de (A;1) (M;1) (B;2) (C;4)
1+1+2+4=8
8 différent de 0 donc Q existe et est unique

Q vérifie : QA + QM + 2QB + 4QC = 0
équivaut à QM + MA + QM + 2QM + 2MB+ 4QM + 4 MC = 0
équivaut à 8QM + MA + 2MB + 4MC = 0

Donc M barycentre de (A;1) (B;2) (C;4) D'ou M = Q

ES ce que c'est bon ?

De plus comment fait-on la question 3 s'il vous plait ?

Merci d'avance.

Non.
bogos13

QA + QM + 2QB + 4QC = 0
Remplace simplement Q par M dans cette relation (puisque l'énoncé précise M=Q).

Bonjour, merci de m'avoir répondu.

De plus pouvez vous m'expliquer et m'aider pour la question 3 s'il vous plait.

Merci d'avance.

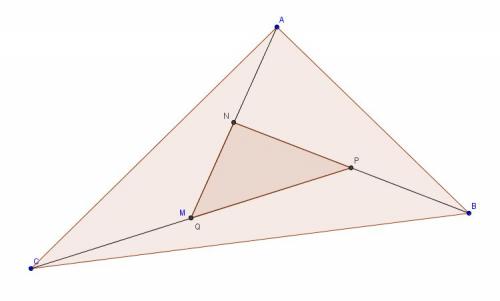
barycentre et aire dans un triangle

Hummm ...

J'ai une piste à exploiter ...

Saurais-tu expliquer pourquoi :

AMC et AMP ont la même aire
ainsi que BNA et BNM
et aussi CPB et CBN

Ces paires de triangles ont des hauteurs communes n'est-ce-pas ?

Bonsoir, merci de m'avoir répondu.

En effet, je vois que ces triangles ont des hauteurs communes.
Mais je ne sais pas expliqué pourquoi.
Pouvez vous m'expliquer et m'aider s'il vous plait.

Merci d'avance.

Tu sais ce qu'est une hauteur non ? Donne m'en la définition.

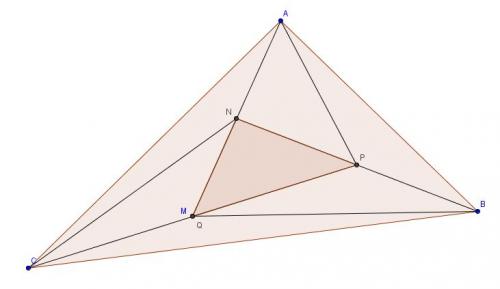
$fichier math$
Vois-tu pourquoi 7 triangles dans le triangle ABC ont tous la même aire ?

Bonsoir, merci de m'avoir répondu.

Hauteur : on appelle hauteur issue de A dans le triangle ABC, la droite notée A qui passe par A et qui est perpendiculaire à la droite (BC).

Je vois bien 7 triangles dans le triangle ABC. Oui ils ont tous la même aire. Mais qu'elle rédaction faut-il faire pour démontrer cela ?
Pouvez vous m'aider s'il vous plait.

Merci d'avance.

Oui pour la hauteur. Donc dès lors que deux triangles ont un sommet commun et une base commune, ils ont une hauteur commune.

Rappelle-toi la formule permettant de calculer l'aire d'un triangle.
Comprends-tu pourquoi MPN et MPB ont la même aire ?

Bonjour. Merci de m'avoir répondu.

bxh/2

MPN et MPB ont la même aire car ils ont une base en commun et donc une hauteur c'est sa ?

Merci d'avance.

Disons plutôt que leurs bases ont même longueur.

Maintenant trouve toutes les paires de triangles de même aire dans le grand triangle.

Bonjour, merci de m'avoir répondu.

Donc alors :
Dans le triangle CNP (NM) est une médiane donc aire (CNM) = aire (NMP)
Dans le triangle AMC (CN) est une médiane donc aire (CNM) = aire (ANC)

Dans le triangle AMP (NP) est une médiane donc aire (ANP) = aire (NMP)
Dans le triangle ABN (AP) est une médiane donc aire (ANP) = aire (APB)
Dans le triangle MNB (MP) est une médiane donc aire (MNP) = aire (MPB)Dans le triangle CPB (QB) est une médiane donc aire (CQN) = aire (QPB)

Voila et après qu'es ce qu'on doit faire ? Pouvez vous m'aider s'il vous plait.

Merci d'avance.

bogos13

Dans le triangle CNP (NM) est une médiane donc aire (CNM) = aire (NMP)
Dans le triangle AMC (CN) est une médiane donc aire (CNM) = aire (ANC)
Que peux-tu donc dire des aires de MNP et de ANC ?

Bonjour, merci de m'avoir répondu.

On peut dire qu'ils ont la même aire.
C'est ça ?

Merci d'avance.

Oui. Tu dois ainsi trouver qu'ils ont tous la même aire.

Bonjour, merci de m'avoir répondu.

Je ne comprendpas comment il faut raisonner.
Pouvez vous m'expliquer s'il vous plait.

Merci d'avance.

Tu dois raisonner pour tous les triangles comme tu l'as fait pour MNP et ANC.

Bonjour,

alors :
Dans le triangle AMP (NP) est une médiane donc aire (ANP) = aire (NMP)
Dans le triangle ABN (AP) est une médiane donc aire (ANP) = aire (APB)
Donc le triangle NMP et APB ont la même aire

Dans le triangle MNB (MP) est une médiane donc aire (MNP) = aire (MPB)Dans le triangle CPB (QB) est une médiane donc aire (CQN)= aire (QPB)
Donc le triangle MPB et QPB ont la même aire

Je sais pas si c'est sa ?

Merci d'avance.

Bah il s'agit d'utiliser la transitivité : si a=b et b=c alors a=b=c
Trouve des triplets (a,b,c) de triangles de même aire.

Ici ça marche :
bogos13
Dans le triangle AMP (NP) est une médiane donc aire (ANP) = aire (NMP)
Dans le triangle ABN (AP) est une médiane donc aire (ANP) = aire (APB)
Donc le triangle NMP et APB ont la même aire

Là je ne te comprends pas :
bogos13
Dans le triangle MNB (MP) est une médiane donc aire (MNP) = aire (MPB)Dans le triangle CPB (QB) est une médiane donc aire (CQN)= aire (QPB)
Donc le triangle MPB et QPB ont la même aire

Bonjour, merci de m'avoir répondu.

Alors : ANC = CNM = ANP
CMB = CNM = MNP
PAB = PAN = PBM
PAB = PQN = PQB

Es ce que c'est comme ça ?

Merci d'avance.

Bonsoir, pouvez vous m'aider et m'expliquer s'il vous plait.

Merci d'avance.