Thalès, périmètre et étude d'une fonction

Sur la figure, ABC et AMN sont deux triangles isocèles en A. Les points A, M, B d'une part et A, N, C d'autre part sont alignés. De plus, (MN) // (BC)

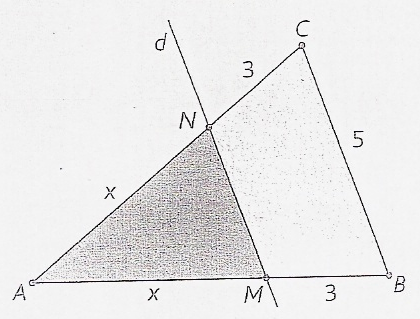
$fichier math$

Exprimer en fonction de x la longueur MN
Déduire de la question précédente que le périmètre p(x) du trapèze MBCN est donné par : p(x) = 16x + 33 / x + 3
Tracer la courbe représentative sur la calculatrice et conjecturer le sens de variation sur l'intervalle [0;10]
a. Démontrer que pour tout x ∈[0;10] :
p(x) = 16 - 15/ x + 3
b. Démontrer la conjecture du 3
Est-il possible d'avoir p(x) = 15 ? Justifier.

J'ai su faire les question 1 et 3 mais j'ai besoin d'aide pour les autres . .

Re bonsoir

qu'as tu trouvé à la 1) ?

Tu as trouvé la question 2) ?
p(x) = (16x+33) / (x+3)

Pour la 4), pars de, pour tout x∈[0;10], x+3≠0 et

16 - 15/(x+3) = ...
en mettant tout au même dénominateur (x+3) et montre que tu aboutis à (16x+33) / (x+3) c'est à dire à p(x)

A la 1, j'ai trouvé : MN = 5x/x+3

A la 2, j'ai le raisonnement, mais je n'arrive pas à m'en serve pour trouver la répondre.

& pour la 4a, je ne vois pas . .

& donc la 5 : p(x) = 15
16-15/x+3 = 15
16-15/x+3 = 15x+45/x+3 ?

MN = 5x/(x+3) c'est ok
le périmètre p(x) = MN + 3 + 5 +3 = (5x)/(x+3) + 11 = ...

en mettant 11 au même dénominateur (x+3) et en réduisant tu devrais t'en sortir.

4a)
x≥0 car c'est une longueur, donc x+3≠0
calcule 16 - 15/(x+3) = 16(x+3)/(x+3) - 15/(x+3) = ...

MN + 3 + 5 +3
= (5x)/(x+3) + 11
= (5x)/(x+3) + (11x+33)/(x+3)
= 5x+11x+33/(x+3)
= 16x+33/x+3
la courbe est croissante ?

4a) 2tant donné que nous trouvons (x+3) au numérateur et dénominateur, cela donne onc 16-15/x+3 ?

Bonsoir,

Sur l'intervalle [0;10], la fonction p est croissante.
Pour le 4)
soit tu poursuis le calcul indiqué par Iron, 16 - 15/(x+3) = 16(x+3)/(x+3) - 15/(x+3) = ...
soit tu écris p(x) = (16x+33 +15-15)/(x+3) = ....

Mais est ce normal si pour la 4b. j'arrive à la conclusion que la courbe du 3 est décroissante ?

Comment trouves-tu que la fonction est décroissante ?

p(x) = 16x+33/x+3

Donc : si x = 0 : p(0) = 160+33/0+3 = 33/3 = 11
si x = 10 : p(10) = 1610+33/10+3 = 193/13≈15
Elle est croissante, c'est une erreur de ma part, désolée.

Pour démontrer la conjecture, utilise la forme p(x) = 16 - 15/x+3
Et si x1 > x2 > 0
compare f(x1) avec f(x2)

Mais qu'est ce que (fx1) et f(x2) ?

C'est p(x1) et p(x2)

Je ne comprends absolument rien . .

Applique le même raisonnement que l'exercice sur les fonctions du second degré.

Donc pour commencer : p(x) = 16-15/x+3
0 ≤ x ≤ 10 ?

Oui

p(x) = 16-15/(x+3)
0 ≤ x1 ≤ x2 ≤ 10
...

0≤x1≤x2≤10
J'ajoute 3 :
3≤(x1+3)≤(x2+3)≤13
Fonction inverse :
1/3≥1/(x1+3)≥1/(x2+3)≥1/13
Multiplier par -15 ?
-5≤-5/x1+3≤-5/x2+3≤-1
Ajouter 16 ?
11≤16-5/x1+3≤16-5/x2+3≤15 ?

Je corrige sur ta réponse :

0≤x1≤x2≤10
J'ajoute 3 :
3≤(x1+3)≤(x2+3)≤13
Fonction inverse :
1/3≥1/(x1+3)≥1/(x2+3)≥1/13
Multiplier par -15 ?
-5≤-15/x1+3≤-15/x2+3≤-15/13
Ajouter 16 ?
11≤16-15/(x1+3)≤16-15/(x2+3)≤16 -15/13
Soit
11 ≤p(x1) ≤p(x2)≤ 16-15/13
donc pour conclure sur les variations
....

Donc la fonction p est croissante ?

Oui
Sur cet intervalle p est croissante.

D'accord, merci