coordonnées cartésiennes
-
BBlarg dernière édition par
Bonjour,
J'ai un exercice de maths que je n'arrive pas à faire. Pouvez-vous m'aider ? s'il vous plaît.On se place dans un repère orthonormé (O;vect i;vect j) direct.
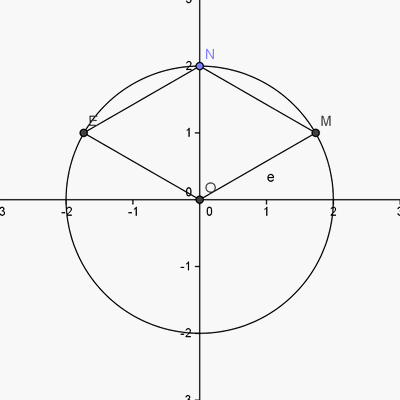
M a pour coordonnées cartésiennes (√3;1) ; r est la rotation de centre O et d'angle π/3. On note N l'image de M par la rotation r et E le point tel que NEMO est un parallélogramme.
Quelle conjecture peut-on faire à propos des coordonnées de N et E ?
Calculer (en justifiant) les coordonnées cartésiennes de E.J'ai fait une figure mais je ne sais pas si mon point M est bien placé.
Merci d'avance !
-
Bonjour,
le point M est bien placé.
Quelle conjecture as tu proposé pour les coordonnées des points N et E ?En prenant le point A (2;0) que peut-on dire du point M ?
-
BBlarg dernière édition par
Bah justement je ne vois pas trop la conjecture que l'on peut faire entre ces deux points.
Le point E a la même abscisse que le point M. De même pour le point N avec le point O.Pour le point M, je ne sais pas non plus.
-
Le point N est sur quel axe ? donc c'est coordonnées .....
Que peut-on dire du point M par rapport au point E ? même ordonnée ....
-
BBlarg dernière édition par
Le point N est sur l'axe des ordonnées. N(0;2) et E(-√3;1)
Pour la conjecture, il fallait juste lire les coordonnées des points N et E graphiquement ?
-
Pour la conjecture :
Le point N est sur l'axe des ordonnées et le point E est le symétrique du point M par rapport à l'axe .....
-
BBlarg dernière édition par
à l'axe des ordonnées
-
Oui.
-
BBlarg dernière édition par
Pour calculer les coordonnées de E, je fais comment ?
-
Utilise une propriété du parallélogramme.
par exemple vect OM = vect EN.
-
BBlarg dernière édition par
N l'image de M par la rotation r.
Puisque vect OM = vect EN. [EN] est l'image de [OM] par la rotation r.
Donc les coordonnées de E ont la même ordonnée que M mais l’abscisse opposée donc E(-√3;1)
-
Non, EN n'est pas l'image de OM par rapport à la rotation r.
-
BBlarg dernière édition par
je ne vois pas comment faire
-
A partir des coordonnées des vecteurs.
-
BBlarg dernière édition par
c'est à dire ?
-
vect OM = vect EN
vect OM ( ..... ; .....)
vect EN ( ..... ; .....)
-
BBlarg dernière édition par
vect OM (√3;1)
vect EN (√3;1)
-
Ecris vecteur EN en fonction des coordonnées de E (x;y)?
-
BBlarg dernière édition par
EN (0-x;2-y)
-
Oui,
et comme vect EN : (√3;1)
tu déduis x et y.